题目内容
已知等差数列{an}的前n项和是Sn=2n2-25n,试求数列{|an|}的前10项的和.
①n=1时,a1=S1=-23.
S2=8-50=-42,
a2=S2-a1=-19,
∴d=a2-a1=4,
∴an=Sn-Sn-1=4n-27,
an<0 得 n≤6,
即数列的前6项为负,则数列{|an|}的前6项的和为数列{an}的前6项的和的相反数,即为-S6=-(2×36-25×6)=78
从第七项开始数列为正,a7=1,a8=5,a9=9,a10=13
数列{|an|}的前10项的和为-S6+a 7+a 8+a 9+a 10=78+1+5+9+13=106.
S2=8-50=-42,
a2=S2-a1=-19,
∴d=a2-a1=4,
∴an=Sn-Sn-1=4n-27,
an<0 得 n≤6,
即数列的前6项为负,则数列{|an|}的前6项的和为数列{an}的前6项的和的相反数,即为-S6=-(2×36-25×6)=78
从第七项开始数列为正,a7=1,a8=5,a9=9,a10=13
数列{|an|}的前10项的和为-S6+a 7+a 8+a 9+a 10=78+1+5+9+13=106.

练习册系列答案
相关题目
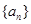 的前
的前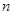 项和
项和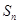 和通项
和通项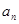 满足
满足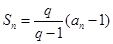 (
(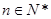 ,
,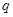 是大于0的常数,且
是大于0的常数,且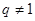 ),数列
),数列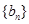 是公比不为
是公比不为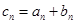 .
.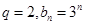 ,是否存在实数
,是否存在实数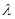 ,使数列
,使数列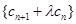 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数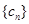 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的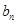 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.