题目内容
已知数列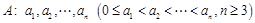 具有性质
具有性质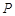 :
:
对任意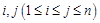 ,
,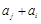 与
与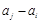 两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列
两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列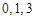 具有性质
具有性质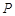 ; ②数列
; ②数列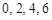 具有性质
具有性质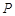 ;
;
③若数列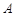 具有性质
具有性质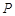 ,则
,则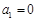 ;
;
④若数列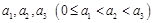 具有性质
具有性质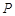 ,则
,则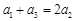 .
.
其中真命题有 .
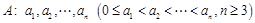 具有性质
具有性质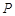 :
:对任意
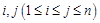 ,
,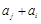 与
与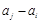 两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列
两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列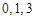 具有性质
具有性质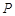 ; ②数列
; ②数列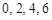 具有性质
具有性质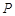 ;
;③若数列
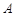 具有性质
具有性质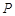 ,则
,则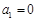 ;
; ④若数列
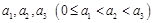 具有性质
具有性质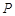 ,则
,则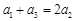 .
.其中真命题有 .
②③④
试题分析:①数列
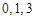 不具有性质
不具有性质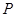 ,因为
,因为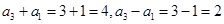 都不是该数列中的数,故①不正确;
都不是该数列中的数,故①不正确;②数列
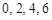 具有性质
具有性质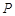 ,因为
,因为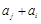 与
与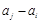 两数中至少有一个是该数列中的一项;
两数中至少有一个是该数列中的一项;③若数列
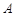 具有性质
具有性质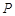 ,对任意
,对任意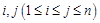 ,
,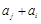 与
与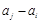 两数中至少有一个是该数列中的一项,选择
两数中至少有一个是该数列中的一项,选择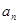 和
和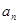 ,则
,则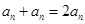 与
与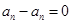 两数中至少有一个是该数列中的一项,因为
两数中至少有一个是该数列中的一项,因为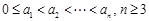 ,很明显
,很明显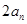 不是该数列中的项,所以0是该数列中的项,则只能
不是该数列中的项,所以0是该数列中的项,则只能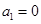 ,故③正确;
,故③正确;④若数列
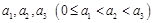 具有性质
具有性质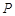 ,所以
,所以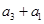 与
与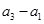 至少有一项是该数列中的一项,且
至少有一项是该数列中的一项,且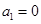 ,
,若
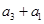 是该数列中的一项,则
是该数列中的一项,则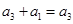 ,
,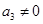
易知
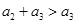 (
(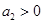 )不是该数列的项,
)不是该数列的项,所以
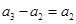 (若
(若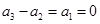 ,则
,则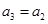 ,这与
,这与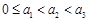 ;若
;若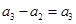 ,则
,则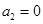 ),所以
),所以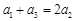 .
.若
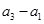 是该数列中的项,则
是该数列中的项,则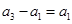 或
或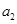 或
或 ,
,若
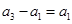 ,则
,则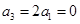 矛盾;
矛盾;若
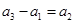 ,则
,则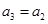 ,与
,与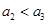 矛盾;
矛盾;若
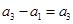 同(1),
同(1),综上
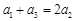 ,故④正确.
,故④正确.
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
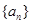 的前n项和为
的前n项和为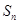 ,且
,且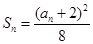 。
。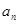 ;
;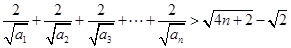 。
。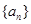 的前
的前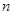 项和
项和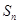 和通项
和通项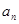 满足
满足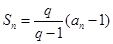 (
(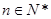 ,
,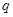 是大于0的常数,且
是大于0的常数,且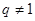 ),数列
),数列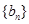 是公比不为
是公比不为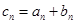 .
.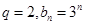 ,是否存在实数
,是否存在实数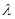 ,使数列
,使数列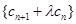 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数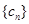 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的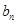 的组合,若不能,请说明理由.
的组合,若不能,请说明理由. 的前
的前 项和
项和 ,那么这个数列的通项公式是 ( )
,那么这个数列的通项公式是 ( )



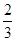 an+
an+ ,则数列{an}的通项公式是an=______.
,则数列{an}的通项公式是an=______.
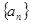 满足:
满足: (
( ),且
),且 ,若数列的前2011项之和为2012,则前2012项的和等于
,若数列的前2011项之和为2012,则前2012项的和等于