题目内容
已知数列{an}满足an = nkn(n∈N*,0 < k < 1),下面说法正确的是( )
①当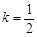 时,数列{an}为递减数列;
时,数列{an}为递减数列;
②当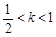 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;
③当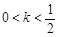 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当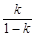 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.
①当
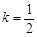 时,数列{an}为递减数列;
时,数列{an}为递减数列;②当
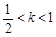 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;③当
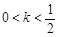 时,数列{an}为递减数列;
时,数列{an}为递减数列;④当
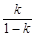 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.| A.①② | B.②④ | C.③④ | D.②③ |
C
试题分析:选项①:当
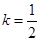 时,
时,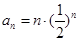 ,有
,有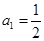 ,
,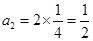 ,则
,则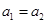 ,即数列
,即数列 不是递减数列,故①错误;
不是递减数列,故①错误;选项②:当
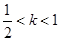 时,
时,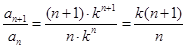 ,因为
,因为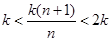 ,所以数列
,所以数列 可有最大项,故②错误;
可有最大项,故②错误;选项③:当
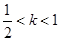 时,
时,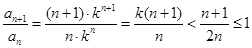 ,所以
,所以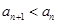 ,即数列
,即数列 是递减数列,故③正确;
是递减数列,故③正确;选项④:
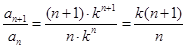 ,当
,当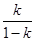 为正整数时,
为正整数时,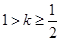 ;当
;当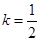 时,
时,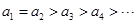 ;当
;当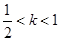 时,令
时,令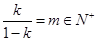 ,解得
,解得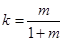 ,
,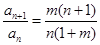 ,数列
,数列 必有两项相等的最大项,故④正确.
必有两项相等的最大项,故④正确.所以正确的选项为③④.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
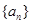 的前n项和为
的前n项和为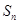 ,且
,且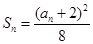 。
。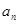 ;
;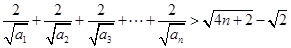 。
。 ,则其前6项之和是( )
,则其前6项之和是( ) 中,
中,
 是等比数列, 求实数
是等比数列, 求实数 ;
; 项和
项和 .
.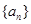 的前
的前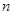 项和
项和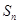 和通项
和通项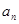 满足
满足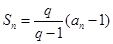 (
(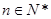 ,
,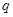 是大于0的常数,且
是大于0的常数,且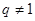 ),数列
),数列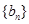 是公比不为
是公比不为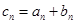 .
.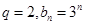 ,是否存在实数
,是否存在实数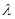 ,使数列
,使数列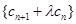 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数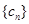 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的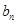 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.