题目内容
已知公差大于零的等差数列{an}的前n项和为Sn,且满足:a3·a4=117,a2+a5=22.
(1)求通项an;
(2)若数列{bn}满足bn=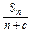 ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
(1)求通项an;
(2)若数列{bn}满足bn=
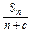 ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.(1)an=1+(n-1)×4=4n-3(2)c=-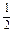
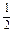
(1)由等差数列的性质得,a2+a5=a3+a4=22,所以a3、a4是关于x的方程x2-22x+117=0的解,又公差大于零,所以a3=9,a4=13.
易知a1=1,d=4,故通项为an=1+(n-1)×4=4n-3.
(2)由(1)知Sn=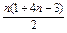 =2n2-n,
=2n2-n,
所以bn=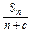 =
=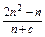 .
.
方法一 所以b1=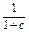 ,b2=
,b2=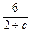 ,b3=
,b3=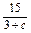 (c≠0).
(c≠0).
令2b2=b1+b3,解得c=-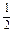 .
.
当c=-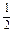 时,bn=
时,bn=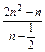 =2n,
=2n,
当n≥2时,bn-bn-1=2.
故当c=-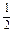 时,数列{bn}为等差数列.
时,数列{bn}为等差数列.
方法二 当n≥2时,
bn-bn-1=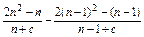
=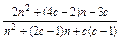 ,
,
欲使{bn}为等差数列,
只需4c-2=2(2c-1)且-3c="2c(c-1)" (c≠0)
解得c=-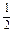 .
.
易知a1=1,d=4,故通项为an=1+(n-1)×4=4n-3.
(2)由(1)知Sn=
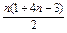 =2n2-n,
=2n2-n,所以bn=
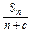 =
=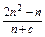 .
.方法一 所以b1=
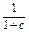 ,b2=
,b2=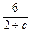 ,b3=
,b3=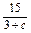 (c≠0).
(c≠0).令2b2=b1+b3,解得c=-
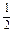 .
.当c=-
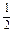 时,bn=
时,bn=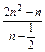 =2n,
=2n,当n≥2时,bn-bn-1=2.
故当c=-
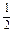 时,数列{bn}为等差数列.
时,数列{bn}为等差数列.方法二 当n≥2时,
bn-bn-1=
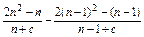
=
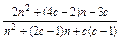 ,
,欲使{bn}为等差数列,
只需4c-2=2(2c-1)且-3c="2c(c-1)" (c≠0)
解得c=-
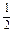 .
.
练习册系列答案
相关题目
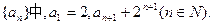
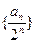 为等差数列;(II)若m为正整数,当
为等差数列;(II)若m为正整数,当
 , ak
, ak ,…, ak
,…, ak ,…成等比数列.
,…成等比数列. 的前n项和Sn.
的前n项和Sn.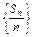 的前n项和,求Tn.
的前n项和,求Tn.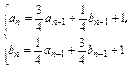 (n≥2).
(n≥2). 中,
中, ,则
,则 ( )
( )


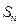 是等差数列
是等差数列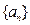 的前n项和,且S3=S8,Sk=S7,则k的值是( )
的前n项和,且S3=S8,Sk=S7,则k的值是( )