题目内容
已知数列{an}、{bn}满足:a1=2,b1=1,
且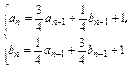 (n≥2).
(n≥2).
(1)令cn=an+bn,求数列{cn}的通项公式;
(2)求数列{an}的通项公式及前n项和公式Sn.
且
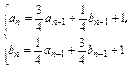 (n≥2).
(n≥2).(1)令cn=an+bn,求数列{cn}的通项公式;
(2)求数列{an}的通项公式及前n项和公式Sn.
(1)cn=3+(n-1)×2=2n+1(2)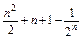
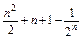
(1)当n≥2时,cn=an+bn=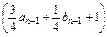 +
+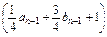 =an-1+bn-1+2,
=an-1+bn-1+2,
∴cn=cn-1+2,即cn-cn-1="2" (n≥2)
∴数列{cn}为等差数列,首项c1=a1+b1=3,公差d=2.
∴cn=3+(n-1)×2=2n+1.
(2)当n≥2时,
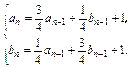

①-②得:an-bn=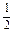 (an-1-bn-1) (n≥2),
(an-1-bn-1) (n≥2),
∴数列{an-bn}为等比数列,首项为a1-b1=1,公比q=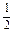 ,
,
∴an-bn=(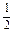 )n-1. ③
)n-1. ③
由(1)知:an+bn="2n+1, " ④
③+④得2an="(2n+1)+" (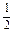 )n-1
)n-1
∴an=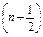 +
+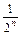
∴Sn=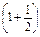 +
+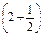 +…+
+…+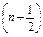 +
+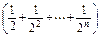
=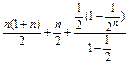
=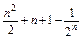 .
.
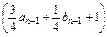 +
+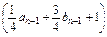 =an-1+bn-1+2,
=an-1+bn-1+2,∴cn=cn-1+2,即cn-cn-1="2" (n≥2)
∴数列{cn}为等差数列,首项c1=a1+b1=3,公差d=2.
∴cn=3+(n-1)×2=2n+1.
(2)当n≥2时,
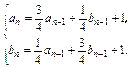

①-②得:an-bn=
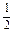 (an-1-bn-1) (n≥2),
(an-1-bn-1) (n≥2),∴数列{an-bn}为等比数列,首项为a1-b1=1,公比q=
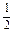 ,
,∴an-bn=(
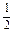 )n-1. ③
)n-1. ③由(1)知:an+bn="2n+1, " ④
③+④得2an="(2n+1)+" (
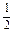 )n-1
)n-1∴an=
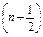 +
+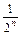
∴Sn=
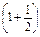 +
+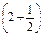 +…+
+…+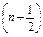 +
+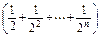
=
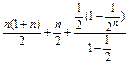
=
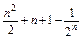 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
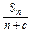 ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.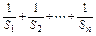 .
.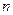 个正数
个正数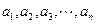 ,使这
,使这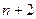 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入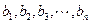 ,使这
,使这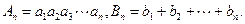 .求:
.求: 和
和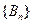 的通项;
的通项;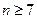 时,比较
时,比较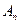 与
与 的大小,并证明你的结论
的大小,并证明你的结论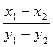 =____________.
=____________.