题目内容
(本小题满分13分) 在数列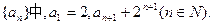
(I)求证:数列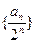 为等差数列;(II)若m为正整数,当
为等差数列;(II)若m为正整数,当
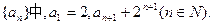
(I)求证:数列
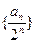 为等差数列;(II)若m为正整数,当
为等差数列;(II)若m为正整数,当
(Ⅰ)见解析 (Ⅱ) 见解析
(I)由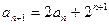 变形得:
变形得: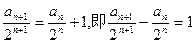
故数列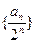 是以
是以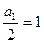 为首项,1为公差的等差数列 (5分)
为首项,1为公差的等差数列 (5分)
(II)(法一)由(I)得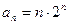
 (7分)
(7分)
令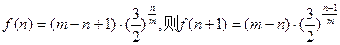
当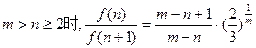
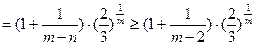
又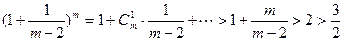
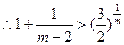 则
则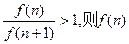 为递减数列。
为递减数列。
当m=n时,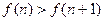
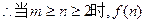 递减数列。(9分)
递减数列。(9分)
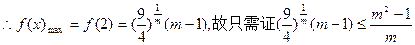
要证: 时,
时,
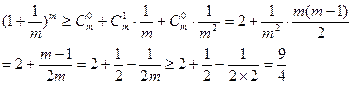
故原不等式成立。 (13分)
(法二)由(I)得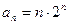
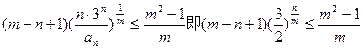 (7分)
(7分)
令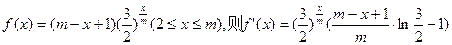
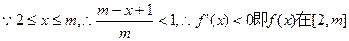 上单调递减。(9分)
上单调递减。(9分)
也即证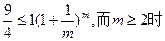 ,
,
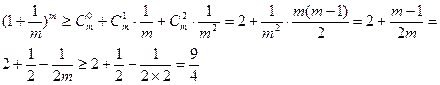
故原不等式成立。(13分)
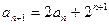 变形得:
变形得: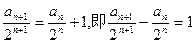
故数列
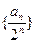 是以
是以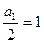 为首项,1为公差的等差数列 (5分)
为首项,1为公差的等差数列 (5分)(II)(法一)由(I)得
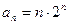
 (7分)
(7分)令
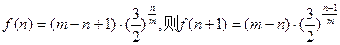
当
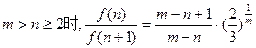
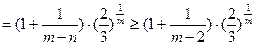
又
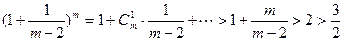
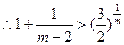 则
则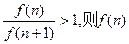 为递减数列。
为递减数列。当m=n时,
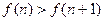
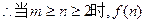 递减数列。(9分)
递减数列。(9分)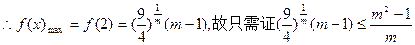
要证:
 时,
时,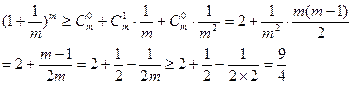
故原不等式成立。 (13分)
(法二)由(I)得
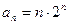
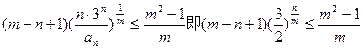 (7分)
(7分)令
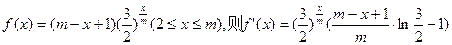
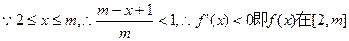 上单调递减。(9分)
上单调递减。(9分)也即证
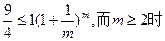 ,
,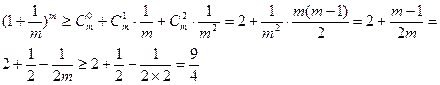
故原不等式成立。(13分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
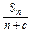 ,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.
,是否存在非零实数c使得{bn}为等差数列?若存在,求出c的值;若不存在,请说明理由.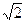 -1,a5=
-1,a5=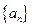 中,设
中,设 .
.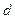 为公差的等差数列,求证
为公差的等差数列,求证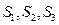 也是等差数列,并求其公差;
也是等差数列,并求其公差;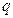 为公比的等比数列,求证
为公比的等比数列,求证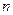 个正数
个正数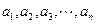 ,使这
,使这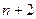 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入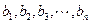 ,使这
,使这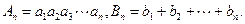 .求:
.求: 和
和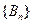 的通项;
的通项;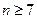 时,比较
时,比较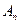 与
与 的大小,并证明你的结论
的大小,并证明你的结论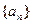 的各项均为正数,其前
的各项均为正数,其前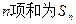 ,且
,且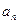 与1的等差中项等于
与1的等差中项等于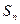 与
与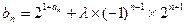 ,且数列
,且数列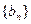 是单调递增数列。试求实数
是单调递增数列。试求实数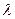 的取值范围。
的取值范围。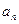 }(
}(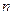 是正整数)是首项是
是正整数)是首项是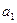 ,公比是
,公比是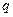 的等比数列。
的等比数列。 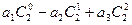 ②
②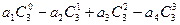
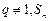 是等比数列的前
是等比数列的前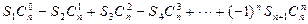
 D
D