题目内容
16.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=3,c=1,sin2A=sinC,则$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{1}{2}$.分析 根据正弦定理以及倍角公式先求出cosA,然后结合余弦定理求出b,利用向量的定义进行求解.
解答 解:∵sin2A=sinC,
∴2sinAcosA=sinC,
即cosA=$\frac{sinC}{2sinA}=\frac{c}{2a}$=$\frac{1}{6}$,
又a2=b2+c2-2bccosA,
即9=b2+1-2b×1×$\frac{1}{6}$,
即3b2-b-24=0,
解得b=3或b=-$\frac{8}{3}$(舍),
则$\overrightarrow{AB}•\overrightarrow{AC}$=bccosA=3×$1×\frac{1}{6}=\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查平面向量数量积的计算,利用正弦定理和余弦定理求出cosA和b是解决本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.已知随机变量ξ服从正态分布,则N(1,4),则P(-3<ξ<1)=( )
参考数据:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.
参考数据:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 0.6826 | B. | 0.3413 | C. | 0.0026 | D. | 0.4772 |
7.某产品的广告费用支出x与销售额y(单位:百万元)之间有如下的对应数据:
(1)求y与x之间的回归直线方程;(参考数据:22+42+52+62+82=145,2×30+4×40+5×60+6×50+8×70=1380)
(2)试预测广告费用支出为1千万元时,销售额是多少?
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费用支出为1千万元时,销售额是多少?
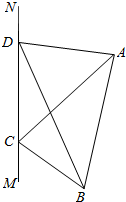 如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
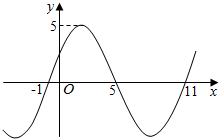 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.