题目内容
11.过点A(1,2),且与直线x-2y+3=0垂直的直线方程为2x+y-4=0.分析 由垂直关系可得直线的斜率,可得点斜式方程,化为一般式即可.
解答 解:∵直线x-2y+3=0的斜率为$\frac{1}{2}$,
∴由垂直关系可得要求直线的斜率为-2,
∴方程为y-2=-2(x-1)
化为一般式可得2x+y-4=0
故答案为:2x+y-4=0
点评 本题考查直线的一般式方程和垂直关系,属基础题.

练习册系列答案
相关题目
2.把一段长为12的细铁丝锯成两段,各自围成一个正三角形,那么这两个正三角形的面积之和的最小值是( )
| A. | $2\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | 4 |
3.A={x||x-1|≥1,x∈R},B={x|log2x>1,x∈R},则“x∈A”是“x∈B”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分也非必要条件 |
20.已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )
| A. | (1,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-∞,-2) |
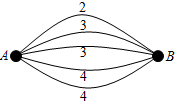 如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.
如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.