题目内容
6．
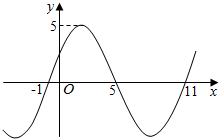函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）在R上的部分图象如图所示，则ω的值为$\frac{π}{6}$．
分析 由函数图象可得周期T=2[5-（-1）]=12，利用周期公式可求ω．
解答 解：由函数图象可得T=2[5-（-1）]=12，
则：$\frac{2π}{ω}$=12，
解得：ω=$\frac{π}{6}$．
故答案为：$\frac{π}{6}$．
点评 本题考查由y=Asin（ωx+φ）的部分图象确定解析式，考查数形结合思想，属基础题．
练习册系列答案
相关题目
14．设非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$，且$|\begin{array}{l}{\overrightarrow{a}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{b}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{c}}\\{\;}\end{array}|$，则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
15．函数f（x）=${log_{\frac{1}{2}}}$x-x+4的零点位于区间（ ）
| A． | $（\frac{1}{2}，1）$ | B． | （1，2） | C． | （2，3） | D． | （3，4） |