题目内容
1.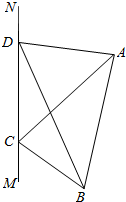 如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.
如图,为对某失事客轮AB进行有效援助,现分别在河岸MN选择两处C、D用强光柱进行辅助照明,其中A、B、C、D在同一平面内.现测得CD长为100米,∠ADN=105°,∠BDM=30°,∠ACN=45°,∠BCM=60°.(1)求△BCD的面积;
(2)求船AB的长.
分析 (1)根据题意求得∠CBD,进而求得BC,BD,进而根据三角形面积公式求得答案.
(2)利用正弦定理求得AD,进而利用余弦定理分别求得BD,AB.
解答 解:(1)由题,∠BDM=30°,∠ACN=45°,∠BCM=60°,
得∠CBD=30°,
所以BC=CD=100,
所以${S_{△BCD}}=\frac{1}{2}CB•CD•sin∠BCD=\frac{1}{2}×100×100×sin{120°}$=$2500\sqrt{3}$平方米.
(2)由题,∠ADC=75°,∠ACD=45°,∠BDA=45°,
在△ACD中,$\frac{CD}{sin∠CAD}=\frac{AD}{sin∠ACD}$,即$\frac{100}{{sin{{60}°}}}=\frac{AD}{{sin4{5°}}}$,
所以$AD=\frac{100}{3}\sqrt{6}$,
在△BCD中,$BD=\sqrt{B{C^2}+C{D^2}-2BC•CDcos∠BCD}=\sqrt{10{0^2}+10{0^2}-2×100×100×cos12{0°}}=100\sqrt{3}$,
在△ABD中,$AB=\sqrt{A{D^2}+B{D^2}-2AD•BDcos∠BDA}$=$\sqrt{{{(\frac{100}{3}\sqrt{6})}^2}+(100\sqrt{3}{)^2}-2×\frac{100}{3}\sqrt{6}×100\sqrt{3}×cos4{5°}}$=$\frac{100}{3}\sqrt{15}$,
即船长为$\frac{100}{3}\sqrt{15}$米.
点评 本题主要考查了正弦定理和余弦定理的运用.解题的重要步骤就是建立数学模型.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
11.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如表所示:
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
附:${Χ^2}=\frac{{n({n_{11}}{n_{22}}-{n_{12}}{n_{21}})2}}{{{n_{11}}{n_{21}}{n_{12}}{n_{22}}}}$
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
附:${Χ^2}=\frac{{n({n_{11}}{n_{22}}-{n_{12}}{n_{21}})2}}{{{n_{11}}{n_{21}}{n_{12}}{n_{22}}}}$
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
12.不等式x2-x-2<0的解集是( )
| A. | {x|x>2} | B. | {x|x<-1} | C. | {x|x<-1或x>2} | D. | {x|-1<x<2} |
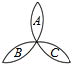 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.