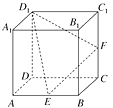
题目内容
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 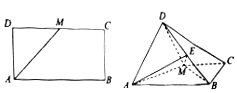
(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
【答案】
(1)证明:∵长方形ABCD中, ![]() ,
, ![]() ,M为DC的中点,
,M为DC的中点,
∴AM=BM=2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM平面ABCM,
∴BM⊥平面ADM,
∵AD平面ADM,∴AD⊥BM
(2)证明:以O为原点,OA为x轴,ON为y轴,OD为z轴,
建立如图所示的直角坐标系
设 ![]() ,则平面AMD的一个法向量
,则平面AMD的一个法向量 ![]() ,
,
![]() =(1﹣λ,2λ,1﹣λ),
=(1﹣λ,2λ,1﹣λ), ![]() ,
,
设平面AME的一个法向量 ![]() ,
,
则  ,∴
,∴ ![]()
取y=1,得x=0,y=1, ![]() ,∴
,∴ ![]() ,
,
∵ ![]() =
= 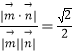 .∴得
.∴得 ![]() 或λ=﹣1,经检验得
或λ=﹣1,经检验得 ![]() 满足题意.
满足题意.
∴E为BD的三等分点.
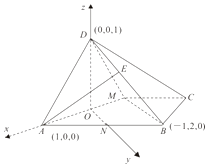
【解析】(1)推导出BM⊥AM,从而BM⊥平面ADM,由此能证明AD⊥BM.(2)以O为原点,OA为x轴,ON为y轴,OD为z轴,建立空间直角坐标系,利用向量法能求出E为BD的三等分点.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目