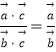Question

【题目】已知cos（π+α）= ，且 ＜α＜π．
（Ⅰ）求5sin（α+π）﹣4tan（3π﹣α）的值
（Ⅱ）若0＜β＜ ，cos（β﹣α）= ，求sin（ +2β）的值．

Answer 1

【答案】解：（Ⅰ）∵cos（π+α）= =﹣cosα，且 ＜α＜π，

∴cosα=﹣ ，sinα= = ，tanα=﹣ ，

∴5sin（α+π）﹣4tan（3π﹣α）=﹣5sinα+4tanα=（﹣5）× +4×（﹣ ）=﹣6．

（Ⅱ）∵0＜β＜ ，cos（β﹣α）= ，

∴﹣π＜β﹣α＜0，可得：sin（β﹣α）=﹣ =﹣ ，

∴cosβ=cos[（β﹣α）+α]=cos（β﹣α）cosα﹣sin（β﹣α）sinα= ×（﹣ ）﹣（﹣ ）× =

∴sin（ +2β）=cos2β=2cos2β﹣1=﹣ ．

【解析】（1）由已知利用诱导公式，通宵三角函数的基本关系式，可得cosα，sinα，tanα，由诱导公式化简即可计算出结果，（2）利用角的范围及同角三角函数基本关系式可得sin（β-α）的值，利用两角和的余弦函数公式可得cosβ=cos[（β﹣α）+α]的值，进而利用诱导公式，二倍角的余弦函数公式即可计算得解.