题目内容
(本题13分)已知抛物线的焦点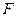 在
在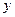 轴上,抛物线上一点
轴上,抛物线上一点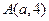 到准线的距离是
到准线的距离是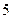 ,过点
,过点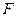 的直线与抛物线交于
的直线与抛物线交于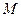 ,
,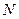 两点,过
两点,过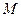 ,
,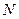 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为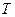 .
.
(1)求抛物线的标准方程;
(2)求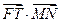 的值;
的值;
(3)求证: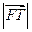 是
是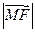 和
和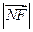 的等比中项.
的等比中项.
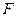 在
在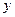 轴上,抛物线上一点
轴上,抛物线上一点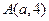 到准线的距离是
到准线的距离是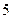 ,过点
,过点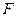 的直线与抛物线交于
的直线与抛物线交于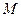 ,
,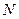 两点,过
两点,过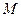 ,
,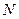 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为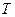 .
.(1)求抛物线的标准方程;
(2)求
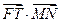 的值;
的值;(3)求证:
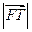 是
是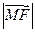 和
和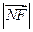 的等比中项.
的等比中项.(1)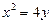
(2)0
(3)证明见解析。
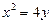
(2)0
(3)证明见解析。
(1)由题意可设抛物线的方程为
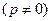 .
.
因为点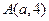 在抛物线上,所以
在抛物线上,所以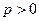 .
.
又点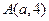 到抛物线准线的距离是
到抛物线准线的距离是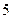 ,所以
,所以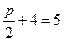 ,可得
,可得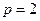 .
.
所以抛物线的标准方程为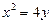 .………………………………………………3分
.………………………………………………3分
(2)解:点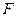 为抛物线的焦点,则
为抛物线的焦点,则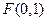 .
.
依题意可知直线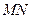 不与
不与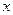 轴垂直,所以设直线
轴垂直,所以设直线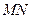 的方程为
的方程为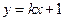 .
.
由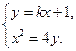 得
得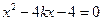 .因为
.因为 过焦点
过焦点 ,所以判别式大于零.
,所以判别式大于零.
设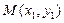 ,
,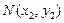 .则
.则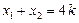 ,
, 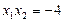 .………………6分
.………………6分
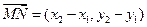
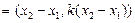 .
.
由于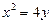 ,所以
,所以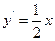 .
.
切线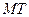 的方程为
的方程为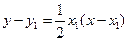 , ①
, ①
切线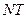 的方程为
的方程为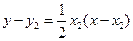 . ②
. ②
由①,②,得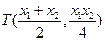 .…………………………………8分
.…………………………………8分
则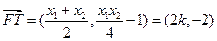 .
.
所以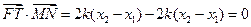 .………………………10分
.………………………10分
(3)证明: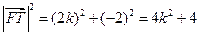 .
.
由抛物线的定义知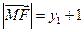 ,
,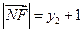 .
.
则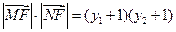
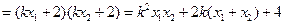
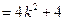 .所以
.所以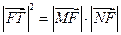 .
.
即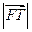 是
是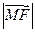 和
和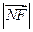 的等比中项.…………………………………………………13
的等比中项.…………………………………………………13

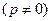 .
.因为点
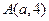 在抛物线上,所以
在抛物线上,所以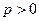 .
.又点
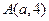 到抛物线准线的距离是
到抛物线准线的距离是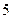 ,所以
,所以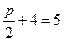 ,可得
,可得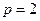 .
.所以抛物线的标准方程为
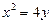 .………………………………………………3分
.………………………………………………3分(2)解:点
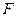 为抛物线的焦点,则
为抛物线的焦点,则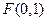 .
.依题意可知直线
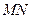 不与
不与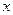 轴垂直,所以设直线
轴垂直,所以设直线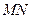 的方程为
的方程为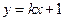 .
.由
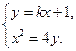 得
得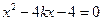 .因为
.因为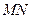 过焦点
过焦点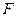 ,所以判别式大于零.
,所以判别式大于零.设
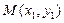 ,
,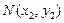 .则
.则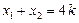 ,
, 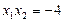 .………………6分
.………………6分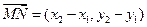
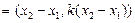 .
.由于
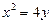 ,所以
,所以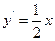 .
.切线
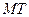 的方程为
的方程为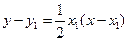 , ①
, ①切线
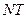 的方程为
的方程为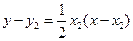 . ②
. ②由①,②,得
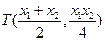 .…………………………………8分
.…………………………………8分则
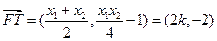 .
.所以
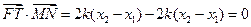 .………………………10分
.………………………10分(3)证明:
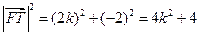 .
.由抛物线的定义知
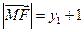 ,
,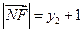 .
.则
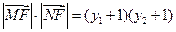
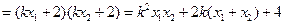
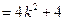 .所以
.所以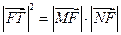 .
.即
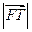 是
是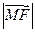 和
和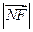 的等比中项.…………………………………………………13
的等比中项.…………………………………………………13
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
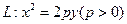 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足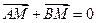 。
。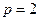 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。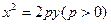 相交于B、C两点,当l的斜率是
相交于B、C两点,当l的斜率是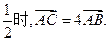
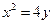 上一点
上一点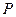 到焦点的距离为2,则点
到焦点的距离为2,则点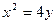 的焦点F作直线交抛物线于
的焦点F作直线交抛物线于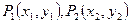 两点,若
两点,若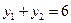 ,则
,则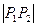 的值为 ( )
的值为 ( ) 的准线方程是 ﹡ .
的准线方程是 ﹡ .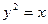 的一条焦点弦,若
的一条焦点弦,若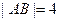 ,则AB的中点到直线
,则AB的中点到直线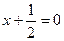 的距离为_______;
的距离为_______;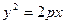 上,横坐标为2的点到抛物线焦点的距离为3,则
上,横坐标为2的点到抛物线焦点的距离为3,则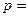 。
。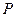 为抛物线
为抛物线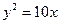 ,则点
,则点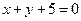 距离的最小值为 。
距离的最小值为 。