题目内容
(12分)已知抛物线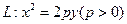 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足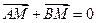 。
。
(1)求实数p的取值范围;
(2)当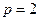 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
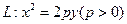 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足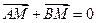 。
。(1)求实数p的取值范围;
(2)当
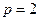 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。 ,存在满足题设的点C,其坐标为(-2,1)。
,存在满足题设的点C,其坐标为(-2,1)。解:(法一)(1)不妨设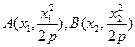 ,且
,且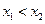 。
。
 。
。
 ,即
,即 ,即
,即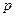 的取值范围为
的取值范围为 。
。
(2)当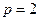 时,由(1)求得A、B的坐标分别为(0,0),(4,4)。假设抛物线L上存在点
时,由(1)求得A、B的坐标分别为(0,0),(4,4)。假设抛物线L上存在点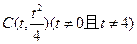 ,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线。设经过A、B、C三点的圆的方程为
,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线。设经过A、B、C三点的圆的方程为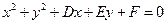 ,则
,则 。
。
整理得 ,①∵函数
,①∵函数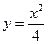 的导数为
的导数为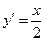 ,∴抛物线L在点
,∴抛物线L在点 处的切线的斜率为
处的切线的斜率为 ,∴经过A、B、C三点的圆N在点
,∴经过A、B、C三点的圆N在点 处的切线斜为
处的切线斜为 。∵
。∵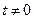 ,∴直线NC的斜率存在。∵圆心N的坐标为
,∴直线NC的斜率存在。∵圆心N的坐标为 ,∴
,∴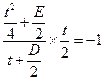 ,即
,即 , ②
, ②
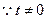 ,由①、②消去E,得
,由①、②消去E,得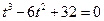 。即
。即 。
。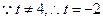 ,故存在满足题设的点C,其坐标为(-2,1)。
,故存在满足题设的点C,其坐标为(-2,1)。
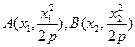 ,且
,且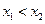 。
。 。
。
 ,即
,即 ,即
,即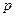 的取值范围为
的取值范围为 。
。(2)当
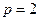 时,由(1)求得A、B的坐标分别为(0,0),(4,4)。假设抛物线L上存在点
时,由(1)求得A、B的坐标分别为(0,0),(4,4)。假设抛物线L上存在点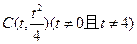 ,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线。设经过A、B、C三点的圆的方程为
,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线。设经过A、B、C三点的圆的方程为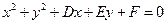 ,则
,则 。
。整理得
 ,①∵函数
,①∵函数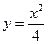 的导数为
的导数为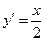 ,∴抛物线L在点
,∴抛物线L在点 处的切线的斜率为
处的切线的斜率为 ,∴经过A、B、C三点的圆N在点
,∴经过A、B、C三点的圆N在点 处的切线斜为
处的切线斜为 。∵
。∵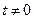 ,∴直线NC的斜率存在。∵圆心N的坐标为
,∴直线NC的斜率存在。∵圆心N的坐标为 ,∴
,∴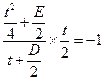 ,即
,即 , ②
, ②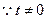 ,由①、②消去E,得
,由①、②消去E,得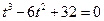 。即
。即 。
。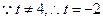 ,故存在满足题设的点C,其坐标为(-2,1)。
,故存在满足题设的点C,其坐标为(-2,1)。
练习册系列答案
相关题目
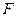 在
在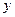 轴上,抛物线上一点
轴上,抛物线上一点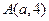 到准线的距离是
到准线的距离是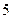 ,过点
,过点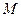 ,
,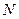 两点,过
两点,过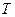 .
.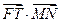 的值;
的值;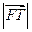 是
是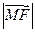 和
和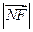 的等比中项.
的等比中项.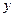 轴上一点
轴上一点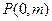 ,斜率为
,斜率为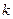 ,两端点A,B到
,两端点A,B到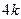
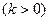 ,
,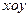 中,直线
中,直线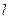 与抛物线
与抛物线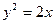 相交于A、B两点。
相交于A、B两点。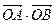 =3”是真命题;
=3”是真命题;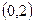 的直线与抛物线
的直线与抛物线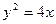 交于不同的两点
交于不同的两点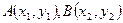 ,计算
,计算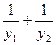 的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:
的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例: 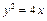 的准线与双曲线
的准线与双曲线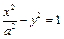 交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率为 .
交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率为 .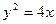 的焦点F交抛物线于A
的焦点F交抛物线于A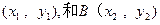 ,
,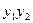 =
= 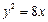 上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是
上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是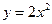 焦点的直线交抛物线于
焦点的直线交抛物线于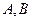 两点,已知
两点,已知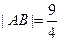 ,
,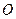 为原点,
为原点,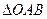 重心的纵坐标为 。
重心的纵坐标为 。