题目内容
(本题满分12分)设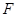 为抛物线
为抛物线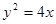 的焦点,
的焦点,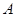 为抛物线上任意一点,已
为抛物线上任意一点,已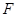 为圆心,
为圆心,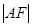 为半径画圆,与
为半径画圆,与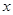 轴负半轴交于
轴负半轴交于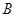 点,试判断过
点,试判断过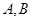 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。
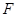 为抛物线
为抛物线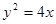 的焦点,
的焦点,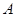 为抛物线上任意一点,已
为抛物线上任意一点,已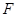 为圆心,
为圆心,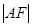 为半径画圆,与
为半径画圆,与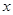 轴负半轴交于
轴负半轴交于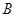 点,试判断过
点,试判断过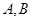 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。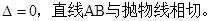
试题分析:解:设

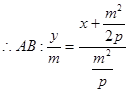 ,即
,即
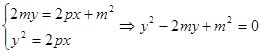
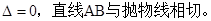
点评:确定直线与圆锥曲线的位置关系的判定,通过联立方程组,结合判别式来判定位置关系,属于重点考点,要掌握。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 中,椭圆
中,椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.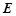 的方程;
的方程; ,
,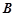 分别是椭圆
分别是椭圆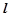 经过点
经过点 轴,点
轴,点 是椭圆上异于
是椭圆上异于 交
交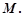

 的斜率为
的斜率为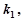 直线
直线 的斜率为
的斜率为 ,求证:
,求证: 为定值;
为定值; 垂直于
垂直于 的直线为
的直线为 .求证:直线
.求证:直线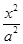 -
- =1的右焦点为
=1的右焦点为 ,则该双曲线的离心率等于( )
,则该双曲线的离心率等于( )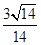 B.
B. C.
C. D.
D.
 上,点Q在曲线C2:(x-2)2+y2=1上,点O为坐标原点,则
上,点Q在曲线C2:(x-2)2+y2=1上,点O为坐标原点,则 的最大值是 .
的最大值是 .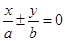 称为椭圆
称为椭圆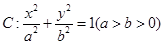 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率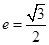 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;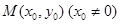 作圆
作圆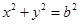 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若 取值范围恰为
取值范围恰为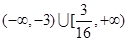 ,求椭圆C的方程.
,求椭圆C的方程.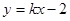 相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
相交于不同的两点A、B,且AB中点横坐标为2,求k的值.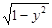 恰有一个公共点,则k的取值范围是___________
恰有一个公共点,则k的取值范围是___________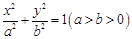 与双曲线
与双曲线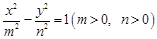 有相同的焦点
有相同的焦点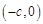 和
和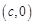 ,若
,若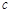 是
是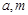 的等比中项,
的等比中项,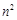 是
是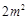 与
与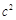 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )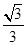
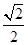
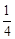
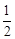

 与
与 轴交于点
轴交于点 ,与直线
,与直线
 交于点
交于点 ,椭圆
,椭圆 以
以 为右焦点,且过点
为右焦点,且过点 时,椭圆
时,椭圆


