题目内容
已知椭圆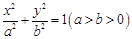 与双曲线
与双曲线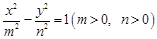 有相同的焦点
有相同的焦点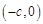 和
和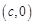 ,若
,若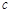 是
是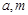 的等比中项,
的等比中项,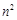 是
是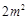 与
与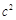 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )
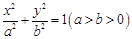 与双曲线
与双曲线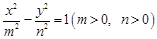 有相同的焦点
有相同的焦点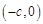 和
和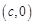 ,若
,若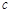 是
是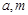 的等比中项,
的等比中项,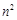 是
是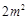 与
与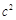 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )A.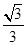 | B.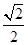 | C.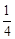 | D.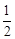 |
D
试题分析:由题意
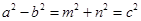 ,
,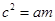 ,
,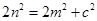 ,∴
,∴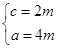 ,∴e=
,∴e=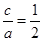 .故选D.
.故选D.点评:由于离心率是c与a的比值,故不必分别求出a、c的值,可寻找a与c的关系式,即a用c来表示即可解决

练习册系列答案
相关题目
题目内容
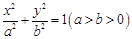 与双曲线
与双曲线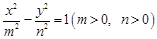 有相同的焦点
有相同的焦点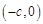 和
和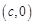 ,若
,若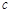 是
是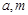 的等比中项,
的等比中项,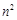 是
是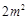 与
与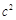 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )A.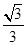 | B.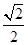 | C.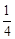 | D.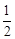 |
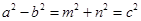 ,
,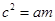 ,
,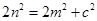 ,∴
,∴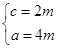 ,∴e=
,∴e=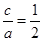 .故选D.
.故选D.