Question

【题目】在平面直角坐标系中，直线与圆相切，圆心的坐标为．

（1）求圆的方程；

（2）设直线与圆没有公共点，求的取值范围；

（3）设直线与圆交于、两点，且，求的值．

Answer 1

【答案】(1) (2) (3) 或．

【解析】

（1）利用直线和圆相切可求圆的半径，从而得到圆的标准方程.

（2）利用圆心到直线的距离大于半径可求的取值范围.

（3）设，由可得，联立直线方程和圆的方程，消去后利用韦达定理化简得到一个与有关的方程，解方程后可求的值.

解：（1）设圆的方程是（为圆的半径），

∵为圆心的圆与直线相切，

∴所求圆的半径，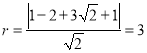

∴所求的圆方程是．

（2）圆心到直线的距离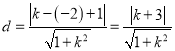

∵与圆没有公共点，

∴即，解得．

的取值范围为.

（3）设

消去，得到方程，

由已知可得，判别式，化简得，

①

由于，可得，

又，

得②

由①②得，故或，它们满足，

故或．