题目内容
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ).
).
(1)求椭圆C的标准方程;
(2)已知直线l不过点P(0,1),与椭圆C交于A、B两点,记直线PA、PB的斜率分别为k1、k2,且满足k1+k2=1,求证:直线l过定点,并求出该定点坐标.
【答案】(1)![]() ;(2)证明详见解析;该定点坐标为
;(2)证明详见解析;该定点坐标为![]() .
.
【解析】
(1)由离心率为![]() 即
即![]() ,又
,又![]() ,得
,得![]() ,再由椭圆经过点M(1,
,再由椭圆经过点M(1,![]() ),可求出椭圆C的标准方程.
),可求出椭圆C的标准方程.
(2)设![]() ,
,![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,由直线
,由直线![]() 的方程与椭圆方程联立解得
的方程与椭圆方程联立解得![]() 点坐标,同理解得
点坐标,同理解得![]() 点坐标,从而求出直线l的斜率,得出l方程,求出直线l所过的定点.
点坐标,从而求出直线l的斜率,得出l方程,求出直线l所过的定点.
解:(1).设椭圆焦距为![]() ,则
,则![]() ,又
,又![]() ,得
,得![]() ,
,
所以![]() 的方程化为
的方程化为![]() ,将
,将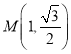 代入有
代入有![]() 解得
解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2).设![]() ,
,![]() .设直线
.设直线![]() 的方程为
的方程为![]()
由![]() 与椭圆方程
与椭圆方程![]() 联立,得
联立,得![]()
化简得:![]()
解得![]() ,
,![]() ,
,
同理,解得![]() ,
,![]() .
.
所以直线![]() 的斜率为
的斜率为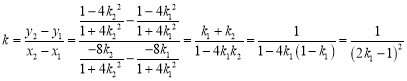 ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
即 ![]() (*).
(*).
取![]() ,得直线
,得直线![]() ,
,
取![]() ,得直线
,得直线![]() ,联立两直线解得交点
,联立两直线解得交点![]() ,
,
经检验,![]() 符合方程(*),所以直线
符合方程(*),所以直线![]() 过定点
过定点![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】2018年开始,直播答题突然就火了,在某场活动中,最终仅有23人平分100万奖金,这23人可以说是“学霸”级的大神.但随着直播答题的发展,其模式的可持续性受到了质疑,某网战随机选取500名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 180 | 140 |
认为直播答题模式不可持续 | 120 | 60 |
(1)根据表格中的数据,用独立性检验的思维方法判断是否有97.5%的把握认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的500人中,有15%曾参加答题游戏瓜分过奖金,而男性被调查者有12%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式:![]()
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
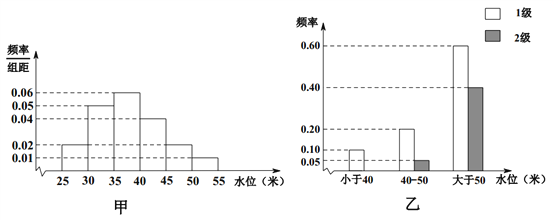
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.