题目内容
6.已知函数 f(x)=$\left\{{\begin{array}{l}{{{(x-1)}^3}(x≥1)}\\{{{(1-x)}^3}({x<1})}\end{array}}$,若关于x的不等式f(x)<f(ax+1)的解集中有且仅有两个整数,则实数a的取值范围为( )| A. | $(-\frac{2}{3},1)$ | B. | $[{-\frac{2}{3},-\frac{1}{2}})∪({\frac{1}{2},\frac{2}{3}}]$ | C. | $({-\frac{2}{3},\frac{2}{3}})$ | D. | $({-\frac{2}{3},\frac{1}{3}})∪(\frac{1}{2},\frac{2}{3})$ |
分析 作出函数f(x)=$\left\{{\begin{array}{l}{{{(x-1)}^3}(x≥1)}\\{{{(1-x)}^3}({x<1})}\end{array}}$的图象,从而可得|x-1|<|ax|,再作出函数y=|x-1|与函数y=|ax|的图象,从而由排除法确定a的取值范围.
解答 解:由题意,
作出函数f(x)=$\left\{{\begin{array}{l}{{{(x-1)}^3}(x≥1)}\\{{{(1-x)}^3}({x<1})}\end{array}}$的图象如下,
故不等式f(x)<f(ax+1)可化为|x-1|<|ax+1-1|,
即|x-1|<|ax|;
作函数y=|x-1|与函数y=|ax|的图象如下,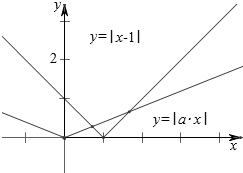
结合图象可得,实数a的取值范围应该关于原点对称,
故排除A、D,
当a=0时,不等式f(x)<f(ax+1)的解集中有且仅有一个整数1,故不正确;
故排除C;
故选:B.
点评 本题考查了分段函数的应用及学生的作图能力,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.$cos(\frac{19π}{3})$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
14.已知△ABC的三边满足(a+b+c)(a+b-c)=($\sqrt{3}$+2)ab,则角C等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
15.cos(-2640°)+sin1665°=( )
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | -$\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1+\sqrt{2}}}{2}$ | D. | -$\frac{{1+\sqrt{2}}}{2}$ |
16. 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )
 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
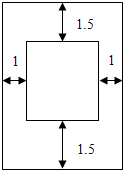 某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?
某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?