题目内容
1．
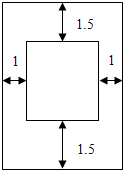某出版社出版一读物，为了排版设计的需要，规定：一页上所印文字的矩形区域需要占去150cm2，上、下边各要留1.5cm宽的空白，左、右两边各要留1cm宽的空白，出版商为了节约纸张，应选用怎样尺寸的矩形纸张来设计版面？
分析 设所印文字的矩形区域的长宽分别为x，$\frac{150}{x}$，求出所选纸张的面积表达式，利用函数的导数通过函数的单调性求解函数y取得最小值．
解答 解：设所印文字的矩形区域的长宽分别为x，$\frac{150}{x}$--（1分）
则所选纸张的面积为$y=（x+2）（\frac{150}{x}+3）$x∈（2，+∞）-------（5分）
$y=3x+\frac{300}{x}+156$，x∈（2，+∞），${y^'}=3-\frac{300}{x^2}=\frac{{3{x^2}-300}}{x^2}$，-------（8分）
当x∈（2，10）时，y′＜0，所以x∈（2，10）时，函数y为减函数，
当x∈（10，+∞）时，y′＞0，所以x∈（2，10）时，函数y为增函数，-------（10分）
所以当x=10时，函数y取得最小值为216，
故应选用长为18，宽为12的矩形纸张来设计版面．-------（12分）
点评 本题考查实际问题的解决，函数的导数的应用，考查转化思想以及计算能力．
练习册系列答案
阅读快车系列答案
相关题目
6．已知函数 f（x）=$\left\{{\begin{array}{l}{{{（x-1）}^3}（x≥1）}\\{{{（1-x）}^3}（{x＜1}）}\end{array}}$，若关于x的不等式f（x）＜f（ax+1）的解集中有且仅有两个整数，则实数a的取值范围为（ ）
| A． | $（-\frac{2}{3}，1）$ | B． | $[{-\frac{2}{3}，-\frac{1}{2}}）∪（{\frac{1}{2}，\frac{2}{3}}]$ | C． | $（{-\frac{2}{3}，\frac{2}{3}}）$ | D． | $（{-\frac{2}{3}，\frac{1}{3}}）∪（\frac{1}{2}，\frac{2}{3}）$ |