题目内容
已知数列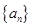 ,
,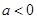 满足
满足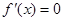 ,
,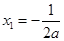 ,
,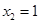 ,
,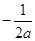 .
.
(1)求证:数列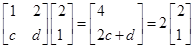 是等差数列,并求数列
是等差数列,并求数列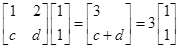 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,对于任意给定的正整数
,对于任意给定的正整数 ,是否存在正整数
,是否存在正整数 ,
,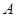 (
(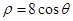 ),使得
),使得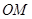 ,
,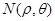 ,
,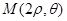 成等差数列?若存在,试用
成等差数列?若存在,试用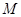 表示
表示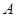 ,
,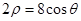 ;若不存在,说明理由.
;若不存在,说明理由.
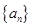 ,
,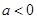 满足
满足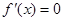 ,
,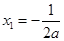 ,
,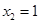 ,
,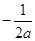 .
.(1)求证:数列
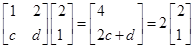 是等差数列,并求数列
是等差数列,并求数列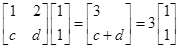 的通项公式;
的通项公式;(2)设数列
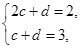 满足
满足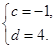 ,对于任意给定的正整数
,对于任意给定的正整数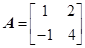 ,是否存在正整数
,是否存在正整数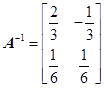 ,
,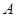 (
(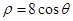 ),使得
),使得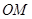 ,
,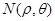 ,
,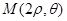 成等差数列?若存在,试用
成等差数列?若存在,试用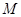 表示
表示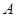 ,
,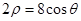 ;若不存在,说明理由.
;若不存在,说明理由.(1)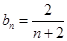 ,(2)当
,(2)当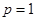 时,不存在
时,不存在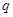 ,
,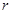 满足题设条件;当
满足题设条件;当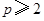 时,存在
时,存在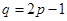 ,
,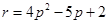 ,满足题设条件.
,满足题设条件.
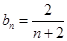 ,(2)当
,(2)当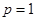 时,不存在
时,不存在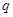 ,
,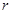 满足题设条件;当
满足题设条件;当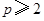 时,存在
时,存在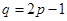 ,
,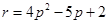 ,满足题设条件.
,满足题设条件.试题分析:(1)求证数列
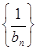 是等差数列,就是确定
是等差数列,就是确定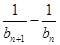 为一个常数.因此首先得到关于
为一个常数.因此首先得到关于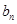 与
与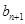 的关系式,因为
的关系式,因为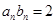 ,所以
,所以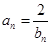 ,则
,则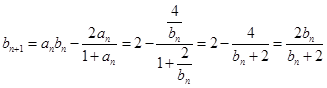 ,然后按提示,将所求关系式进行变形,即取倒数,得:
,然后按提示,将所求关系式进行变形,即取倒数,得: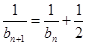 ,又
,又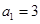 ,所以
,所以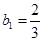 ,故
,故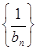 是首项为
是首项为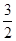 ,公差为
,公差为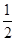 的等差数列,即
的等差数列,即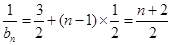 ,所以
,所以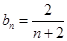 .(2)先明确数列
.(2)先明确数列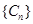 ,由(1)得
,由(1)得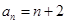 ,所以
,所以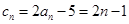 ,然后假设存在,得一等量关系:若
,然后假设存在,得一等量关系:若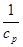 ,
,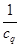 ,
,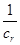 成等差数列,则
成等差数列,则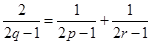 ,如何变形,是解题的关键,这直接影响解题方向.题中暗示,用p表示,所以由
,如何变形,是解题的关键,这直接影响解题方向.题中暗示,用p表示,所以由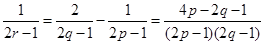 得:
得: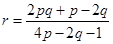 .令
.令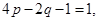 得
得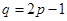 ,因为要
,因为要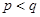 ,所以分情况讨论,当
,所以分情况讨论,当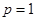 时,
时,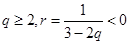 ,
,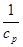 ,
,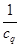 ,
,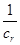 成等差数列不成立.当
成等差数列不成立.当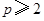 时,
时,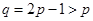 ,
,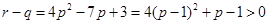 ,即
,即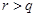 .
.试题解析:(1)因为
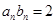 ,所以
,所以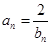 ,
,则
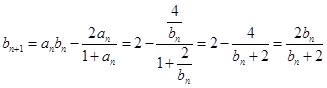 , 2分
, 2分所以
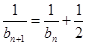 ,
,又
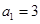 ,所以
,所以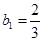 ,故
,故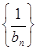 是首项为
是首项为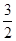 ,公差为
,公差为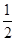 的等差数列, 4分
的等差数列, 4分即
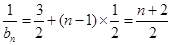 ,所以
,所以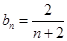 . 6分
. 6分(2)由(1)知
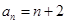 ,所以
,所以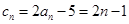 ,
,①当
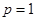 时,
时,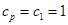 ,
,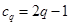 ,
,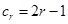 ,
,若
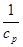 ,
,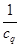 ,
,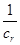 成等差数列,则
成等差数列,则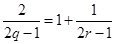 (
(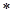 ),
),因为
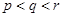 ,所以
,所以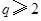 ,
,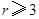 ,
,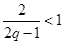 ,
,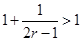 ,
,所以(
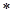 )不成立. 9分
)不成立. 9分②当
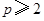 时,若
时,若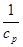 ,
,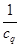 ,
,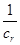 成等差数列,
成等差数列,则
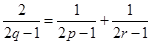 ,所以
,所以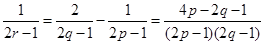 ,
,即
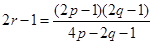 ,所以
,所以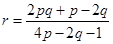 , 12分
, 12分欲满足题设条件,只需
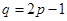 ,此时
,此时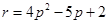 , 14分
, 14分因为
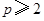 ,所以
,所以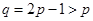 ,
,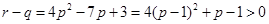 ,
,即
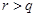 . 15分
. 15分综上所述,当
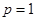 时,不存在
时,不存在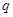 ,
,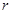 满足题设条件;
满足题设条件;当
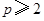 时,存在
时,存在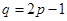 ,
,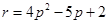 ,满足题设条件. 16分
,满足题设条件. 16分
练习册系列答案
相关题目
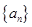 满足
满足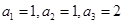 ,若
,若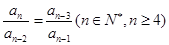 ,则
,则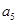 = ,
= ,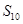 = .
= .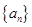 的前n项和为
的前n项和为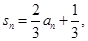 则数列
则数列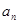 =___ ______ 。
=___ ______ 。 的公比为2,前4项的和是1,则前8项的和为( )
的公比为2,前4项的和是1,则前8项的和为( )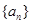 中,已知前n项和
中,已知前n项和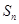 =
=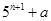 ,则
,则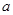 的值为( )
的值为( )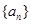 满足:
满足: ,则
,则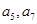 的等比中项为( )
的等比中项为( )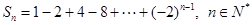 ,则
,则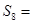 ( )
( )