题目内容
(2011•山东)等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且其中的任何两个数不在下表的同一列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(﹣1)nlnan,求数列{bn}的前2n项和S2n.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(2)若数列{bn}满足:bn=an+(﹣1)nlnan,求数列{bn}的前2n项和S2n.
(1)an=2•3n﹣1,n∈N*.
(2)S2n=32n+nln3﹣1
(2)S2n=32n+nln3﹣1
(1)当a1=3时,不符合题意;
当a1=2时,当且仅当a2=6,a3=18时符合题意;
当a1=10时,不符合题意;
所以a1=2,a2=6,a3=18,
∴公比为q=3,
故:an=2•3n﹣1,n∈N*.
(2)∵bn=an+(﹣1)nlnan
=2•3n﹣1+(﹣1)nln(2•3n﹣1)
=2•3n﹣1+(﹣1)n[ln2+(n﹣1)ln3]
=2•3n﹣1+(﹣1)n(ln2﹣ln3)+(﹣1)nnln3
∴S2n=b1+b2+…+b2n
=2(1+3+…+32n﹣1)+[﹣1+1﹣1+…+(﹣1)2n]•(ln2﹣ln3)+[﹣1+2﹣3+…+(﹣1)2n2n]ln3
=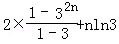
=32n+nln3﹣1
∴数列{bn}的前2n项和S2n=32n+nln3﹣1.
当a1=2时,当且仅当a2=6,a3=18时符合题意;
当a1=10时,不符合题意;
所以a1=2,a2=6,a3=18,
∴公比为q=3,
故:an=2•3n﹣1,n∈N*.
(2)∵bn=an+(﹣1)nlnan
=2•3n﹣1+(﹣1)nln(2•3n﹣1)
=2•3n﹣1+(﹣1)n[ln2+(n﹣1)ln3]
=2•3n﹣1+(﹣1)n(ln2﹣ln3)+(﹣1)nnln3
∴S2n=b1+b2+…+b2n
=2(1+3+…+32n﹣1)+[﹣1+1﹣1+…+(﹣1)2n]•(ln2﹣ln3)+[﹣1+2﹣3+…+(﹣1)2n2n]ln3
=
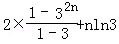
=32n+nln3﹣1
∴数列{bn}的前2n项和S2n=32n+nln3﹣1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 满足
满足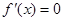 ,
,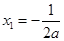 ,
,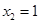 ,
,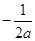 .
.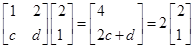 是等差数列,并求数列
是等差数列,并求数列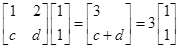 的通项公式;
的通项公式;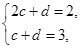 满足
满足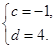 ,对于任意给定的正整数
,对于任意给定的正整数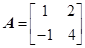 ,是否存在正整数
,是否存在正整数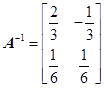 ,
,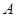 (
(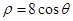 ),使得
),使得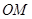 ,
,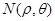 ,
,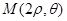 成等差数列?若存在,试用
成等差数列?若存在,试用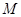 表示
表示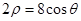 ;若不存在,说明理由.
;若不存在,说明理由.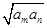 =4a1,则
=4a1,则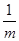 +
+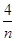 的最小值为________.
的最小值为________.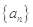 的前
的前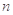 项和为
项和为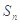 ,且满足
,且满足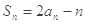 ,
,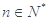
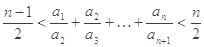
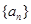 中
中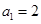 ,公比
,公比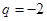 ,记
,记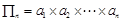 (即
(即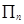 表示数列
表示数列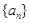 的前n项之积),
的前n项之积),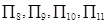 中值最大的是( )
中值最大的是( )

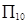

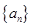 中,已知
中,已知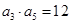 ,则
,则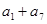 的最小值为 ( )
的最小值为 ( )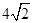
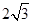
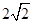

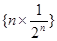 前
前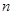 项和
项和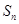 .
. 各项的和为
各项的和为 ,第二项为
,第二项为 ,则该数列的公比为 ( )
,则该数列的公比为 ( ) .
. .
.