题目内容
【题目】“函数![]() 在区间
在区间![]() 上单调”是“函数
上单调”是“函数![]() 在
在![]() 上有反函数”的( )
上有反函数”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分又不必要条件
【答案】A
【解析】
“函数![]() 在区间
在区间![]() 上单调”
上单调”![]() “函数
“函数![]() 在
在![]() 上有反函数”,反之不成立.即可判断出结论
上有反函数”,反之不成立.即可判断出结论
“函数![]() 在区间
在区间![]() 上单调”
上单调”![]() “函数
“函数![]() 在
在![]() 上有反函数”,下面给出证明:
上有反函数”,下面给出证明:
若“函数![]() 在区间
在区间![]() 上单调”,设函数
上单调”,设函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,任取
,任取![]() ,如果在
,如果在![]() 中存在两个或多于两个的
中存在两个或多于两个的![]() 值与之对应,设其中的某两个为
值与之对应,设其中的某两个为![]() ,且
,且![]() ,即
,即![]() ,但
,但![]() .
.
因为![]() ,所以
,所以![]() (或
(或![]() ).
).
由函数![]() 在区间
在区间![]() 上单调知:
上单调知:![]() ,(或
,(或![]() ),这与
),这与![]() 矛盾.因此在
矛盾.因此在![]() 中有唯一的
中有唯一的![]() 值与之对应.由反函数的定义知:
值与之对应.由反函数的定义知:
函数![]() 在区间
在区间![]() 上存在反函数.
上存在反函数.
反之“函数![]() 在
在![]() 上有反函数”则不一定有“函数
上有反函数”则不一定有“函数![]() 在区间
在区间![]() 上单调”,例如:函数
上单调”,例如:函数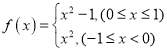 ,就存在反函数:
,就存在反函数: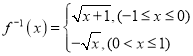
原函数和反函数图象分别如下图(1)(2)所示:
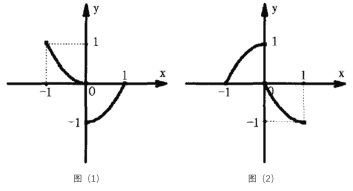
由图象可知:函数![]() 在区间
在区间![]() 上并不单调.
上并不单调.
综上,“函数![]() 在区间
在区间![]() 上单调”是“函数
上单调”是“函数![]() 在
在![]() 上有反函数”的充分不必要条件.
上有反函数”的充分不必要条件.
故选:A.

练习册系列答案
相关题目
