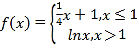题目内容
【题目】已知函数![]() .
.
(1)讨论当![]() 时,函数
时,函数![]() 的单调性;
的单调性;
(2)当![]() 对任意的
对任意的![]() 恒成立,其中
恒成立,其中![]() .求
.求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 为增函数(2)
为增函数(2)![]()
【解析】
(1)将![]() 代入函数解析式,可求得函数解析式及
代入函数解析式,可求得函数解析式及![]() ,由
,由![]() 的单调性及导函数与函数单调性关系即可判断.
的单调性及导函数与函数单调性关系即可判断.
(2)由题意可知![]() 对任意的
对任意的![]() 恒成立,求得
恒成立,求得![]() ,并构造函数
,并构造函数![]() ,求得
,求得![]() ,可判断
,可判断![]() 在
在![]() 上的单调性,从而可得存在
上的单调性,从而可得存在![]() ,使得
,使得![]() ,进而可得
,进而可得![]() ,由
,由![]() 可得方程
可得方程![]() ,代入
,代入![]() 中,可由
中,可由![]() 求得
求得![]() 的取值范围.
的取值范围.
(1)函数![]() ,
,
将![]() 代入,可得
代入,可得![]() ,则
,则![]() ,
,![]() .
.
当![]() 为单调递增函数,
为单调递增函数,![]() ,
,
所以![]() 在
在![]() 为增函数;
为增函数;
(2)由已知有![]() ,其中
,其中![]() ,
,![]() .
.
![]()
![]() .
.
令![]() ,其中
,其中![]() ,
,![]() .
.
由![]() 得
得![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,当
,当![]() 时,
时,![]() ,
,
故存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
故![]()
![]() .
.
由![]() 得,
得,![]() ,即
,即![]() .
.
则![]()
![]()
![]()
![]() .
.
令![]() ,由
,由![]() ,
,![]() ,解得
,解得![]() .
.
因为![]() 在
在![]() 上单调递增,
上单调递增,![]() ,所以
,所以![]() .
.
故![]() ,即
,即![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目
【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.