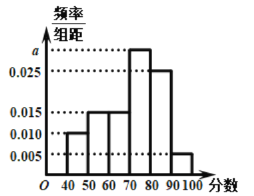
��Ŀ����
����Ŀ��ij�����������ڣ�ÿ������10��ij��Ʒ�����е�һ��ڶ���ֱ�������1��2����Ʒ�����ʼ첿ÿ��Ҫ��������10����Ʒ�������ȡ4�����м�飬�������д�Ʒ������IJ�Ʒ����ͨ��.
��1��������ȫ��ͨ�����ĸ��ʣ�
��2�������ڶԸó��������IJ�Ʒ�������ý����ƶȣ�����ȫ��ͨ����鷣300Ԫ��ͨ��1�죬2��ֱ�300Ԫ900Ԫ.��ô�ó������������ڵõ��������ѧ�����Ƕ���Ԫ��
���𰸡���1��![]() .��2��
.��2��![]() (Ԫ)
(Ԫ)
��������
��1��������ֱ�ɵõ�һ����ͨ�����ĸ��ʣ��ɶ����¼��ĸ��ʹ�ʽ�ɵã�
��2�������ý���Ϊ��Ԫ��������ȡֵΪ��300��300��900���ֱ�������ʿɵ���ѧ����.
��1�������ȡ4����Ʒ���м��������¼�������һ����9����Ʒ���ڶ�����8����Ʒ��
��һ��ͨ�����ĸ���Ϊ![]() .
.
�ڶ���ͨ�����ĸ���Ϊ![]() .
.
��Ϊ��һ��ڶ������Ƿ�ͨ����������ģ�
��������ȫ��ͨ�����ĸ���Ϊ![]() .
.
��2�������ý���Ϊ��Ԫ��������ȡֵΪ��300��300��900 ��
������ɵ�![]() ��
��
![]() .
.
��![]() (Ԫ).
(Ԫ).

����Ŀ����ѧ�о�����������������в��ĸо�������������ǿ��![]() ��λ����
��λ����![]() ƽ����
ƽ����![]() �й�
�й�![]() ��ʵ�ʲ���ʱ������
��ʵ�ʲ���ʱ������![]() ��λ���ֱ�
��λ���ֱ�![]() ����ʾ����ǿ���ĵȼ�������������ǿ��I�����ϵʽ��
����ʾ����ǿ���ĵȼ�������������ǿ��I�����ϵʽ��![]() �dz���
�dz���![]() ������
������![]() ��
��![]() ƽ����
ƽ����![]() ��紵��Ҷɳɳ����ǿ��
��紵��Ҷɳɳ����ǿ��![]() ��
��![]() ƽ���ף�����ǿ���ȼ�
ƽ���ף�����ǿ���ȼ�![]() �ֱ���
�ֱ���
![]() ��֪�����м���������ǿ�������
��֪�����м���������ǿ�������
������Դ
������С | �紵��Ҷɳɳ�� | �������� | �����ӵ���· |
ǿ�� |
|
|
|
ǿ���ȼ� | 10 | m | 90 |
��a��m��ֵ
![]() Ϊ�˲�Ӱ����������Ϣ��˯�ߣ�������ǿ���ȼ�һ�㲻�ܳ���50�ֱ������ʱ����ǿ��I�����ֵ��
Ϊ�˲�Ӱ����������Ϣ��˯�ߣ�������ǿ���ȼ�һ�㲻�ܳ���50�ֱ������ʱ����ǿ��I�����ֵ��
����Ŀ��һ̨����ʹ�õ�ʱ��ϳ�����������ʹ�ã�������ͬ��ת������������ij��е�����һЩ����ȱ�㣬ÿСʱ������ȱ������Ķ��٣����������ת���ٶȶ��仯���±�Ϊ��������Ľ����
ת��x(ת/��) | 2 | 4 | 5 | 6 | 8 |
ÿСʱ������ȱ��������y(��) | 30 | 40 | 60 | 50 | 70 |
��1����ɢ��ͼ��
��2�����y��x��������ع�ϵ����ع�ֱ�߷��̣�
��3����ʵ�������У�����ÿСʱ�IJ�Ʒ����ȱ���������Ϊ89������ô��������ת�ٶ�Ӧ������ʲô��Χ�ڣ�(�ο���ֵ��![]() )
)
����Ŀ��ij����������ŮԱ��500�ˣ��ִ��г�ȡ100λԱ��������ÿ����ɺϸ��Ʒ�ļ���ͳ�����£�
ÿ����ɺϸ��Ʒ�ļ�������λ���ټ��� |
|
|
|
|
|
Ƶ�� | 10 | 45 | 35 | 6 | 4 |
��Ա������ | 7 | 23 | 18 | 1 | 1 |
��1������ÿ����ɺϸ��Ʒ�ļ���������3200����Ա������Ϊ���������֡�.������ͳ��������д����![]() �����������ж��Ƿ���95%�İ�����Ϊ���������֡����Ա��йأ�
�����������ж��Ƿ���95%�İ�����Ϊ���������֡����Ա��йأ�
�ǡ��������֡� | ���������֡� | �ϼ� | |
��Ա�� | |||
ŮԱ�� | |||
�ϼ� |
��2��Ϊ���Ա���Ͷ��Ļ����ԣ�����ʵ���۽��Ƽ������ƣ��涨ÿ����ɺϸ��Ʒ�ļ����ڶ���2600�����ڵģ��Ƽ�����Ϊ1Ԫ������![]() ���IJ��֣��۽��Ƽ�����Ϊ1.2Ԫ������
���IJ��֣��۽��Ƽ�����Ϊ1.2Ԫ������![]() ���IJ��֣��۽��Ƽ�����Ϊ1.3Ԫ������400�����ϵIJ��֣��۽��Ƽ�����Ϊ1.4Ԫ.����4���и��ε�Ƶ����Ϊ��Ӧ�ĸ��ʣ��ڸó���Ա����ѡȡ1�ˣ�ŮԱ�������ѡȡ2�˽��й��ʵ��飬��ʵ�üƼ����ʣ�ʵ�üƼ�����=����Ƽ�����+������Ƽ����ʣ�������3100Ԫ������Ϊ����ķֲ��к���ѧ����.
���IJ��֣��۽��Ƽ�����Ϊ1.3Ԫ������400�����ϵIJ��֣��۽��Ƽ�����Ϊ1.4Ԫ.����4���и��ε�Ƶ����Ϊ��Ӧ�ĸ��ʣ��ڸó���Ա����ѡȡ1�ˣ�ŮԱ�������ѡȡ2�˽��й��ʵ��飬��ʵ�üƼ����ʣ�ʵ�üƼ�����=����Ƽ�����+������Ƽ����ʣ�������3100Ԫ������Ϊ����ķֲ��к���ѧ����.
����![]() ��
��
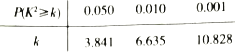 .
.