题目内容
设命题p:函数 f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式a<x+
-1对?x∈(0,+∞)恒成立.如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
| 1 |
| x |
考点:复合命题的真假
专题:简易逻辑
分析:求出命题p,q成立的等价条件,利用“p∨q”为真命题,命题“p∧q”为假命题,则p,q一真一假,分类讨论,确定实数a的取值范围.
解答:
解::命题p:若函数f(x)=lg(ax2-4x+a)的定义域为R,
则ax2-4x+a>0恒成立.
若a=0,则不等式为-4x>0,即x<0,不满足条件,
若a≠0,则
解得a>2,即p:a>2,
命题q:∵x∈(0,+∞),∴x+
-1≥2
-1=1(当且仅当x=
即x=1时取相等)
不等式a<x+
-1对?x∈(0,+∞)恒成立,即为a<1
由题意“p∨q”为真命题,命题“p∧q”为假命题,则p,q一真一假
若p真q假,则
,则a>2,
若p假q真,则
,则a<1,
即实数a的取值范围是a>2或a<1.
则ax2-4x+a>0恒成立.
若a=0,则不等式为-4x>0,即x<0,不满足条件,
若a≠0,则
|
命题q:∵x∈(0,+∞),∴x+
| 1 |
| x |
x×
|
| 1 |
| x |
不等式a<x+
| 1 |
| x |
由题意“p∨q”为真命题,命题“p∧q”为假命题,则p,q一真一假
若p真q假,则
|
若p假q真,则
|
即实数a的取值范围是a>2或a<1.
点评:本题主要考查复合命题与简单命题之间的关系,利用条件先求出p,q成立的等价条件是解决此类问题的关键.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
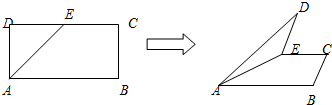
如图,在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将AD折起,使二面角D-AE-B为60°,则异面直线BC与AD所成的角余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=x2-1在下列定区间上是增函数的是( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
下列函数存在极值的是( )
A、y=
| ||
| B、y=x-ex | ||
| C、y=x3+x2+2x-3 | ||
| D、y=x3 |
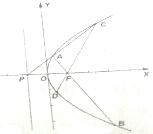 如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且
如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且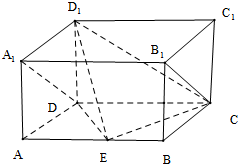 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.