题目内容
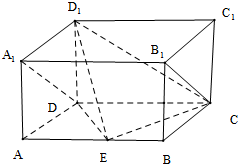 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB的中点.(Ⅰ)求证:B1C⊥平面AED1;
(Ⅱ)求二面角A-D1E-C的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先建立空间直角坐标系,求出相应的点的坐标,利用向量的数量积,求出平面的法向量,进一步利用向量共线求出结果.
(Ⅱ)先求出平面的法向量,利用法向量的夹角求出结果.
(Ⅱ)先求出平面的法向量,利用法向量的夹角求出结果.
解答:
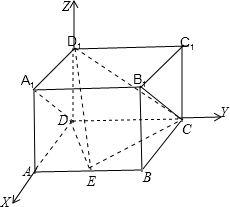
证明:( I)如图,因为ABCD-A1B1C1D1为长方形,以D为坐标原点,DA为x轴的正半轴,DC为y轴的正半轴,建立空间直角坐标系,
由题知,A(1,0,0),E(1,1,0),D1(0,0,1),C(0,2,0),B1(1,2,1);所以
=(-1,0,-1);
设平面AED1的一个法向量为
=(x,y,z),
=(0,1,0),
=(-1,0,1);
由
,则
,令x=1,求得
=(1,0,1);
∵
=-
,
所以,B1C⊥平面AED1成立.
解:( II) 设二面角A-D1E-C的平面角为θ∈[0,π],
由( I) 平面AED1的一个法向量为
=(1,0,1);
同理:设
=(x,y,z)
由于E(1,1,0),C(0,2,0),D1(0,0,1)
=(-1,1,0),
=(0,2,-1)
可求平面D1EC的一个法向量为:
=(-1,-1,-2)
∴cosθ=
=-
,
所以
所以,所求二面角A-D1E-C的平面角为:θ=
由题知,A(1,0,0),E(1,1,0),D1(0,0,1),C(0,2,0),B1(1,2,1);所以
| B1C |
设平面AED1的一个法向量为
| n |
| AE |
| AD1 |
由
|
|
| n |
∵
| n |
| B1C |
所以,B1C⊥平面AED1成立.
解:( II) 设二面角A-D1E-C的平面角为θ∈[0,π],
由( I) 平面AED1的一个法向量为
| n |
同理:设
| n2 |
由于E(1,1,0),C(0,2,0),D1(0,0,1)
| EC |
| D1C |
|
可求平面D1EC的一个法向量为:
| n2 |
∴cosθ=
| ||||
|
|
| ||
| 2 |
所以
所以,所求二面角A-D1E-C的平面角为:θ=
| 5π |
| 6 |

点评:本题考查的知识要点:线面垂直的判定定理,法向量的应用,二面角的应用,属于基础题型.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
已知函数f(x)=
g(x)=
,则函数f[g(x)]的所有零点之和是( )
|
|
A、-
| ||||
B、
| ||||
C、-1+
| ||||
D、1+
|
 △ABC是正三角形,线段EA和DC都垂直与平面ABC,设EA=AB=2α,DC=a,且F为BE的中点,如图:
△ABC是正三角形,线段EA和DC都垂直与平面ABC,设EA=AB=2α,DC=a,且F为BE的中点,如图: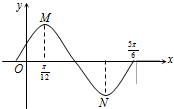 如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<
如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<