题目内容
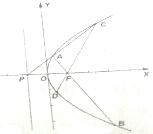 如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且
如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且| AF |
| FB |
| CF |
| FD |
若
| AF |
| CF |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A,C两点的坐标为(x1,y1),(x2,y2),设过P点的直线方程为:x+1=my,即x=my-1,若直线与抛物线y2=4x有两个交点,则联立直线与抛物线方程后的方程y2-4my+4=0的△=16m2-16>0,进而根据韦达定理和向量数量积的定义,构造方程求出m值,可得答案.
解答:
解:由已知可得F点的坐标为(1,0),P点坐标为(-1,0),
设A,C两点的坐标为(x1,y1),(x2,y2),
设过P点的直线方程为:x+1=my,即x=my-1,
则由直线与抛物线y2=4x有两个交点,可得:
y2=4my-4,即y2-4my+4=0的△=16m2-16>0,解得m<-1,或m>1,
且y1+y2=4m,y1•y2=4,
则x1+x2=m(y1+y2)-2=4m2-2,x1•x2=m2y1y2-m(y1+y2)+1=1,
∵
=(1-x1,-y1),
=(1-x2,-y2),
∴
•
=1-(x1+x2)+x1•x2+y1•y2=1-(4m2-2)+1+4=0,
即4m2-8=0,解得m=±
,
故直线l的方程为x+1=±
y,即x±
y+1=0;
设A,C两点的坐标为(x1,y1),(x2,y2),
设过P点的直线方程为:x+1=my,即x=my-1,
则由直线与抛物线y2=4x有两个交点,可得:
y2=4my-4,即y2-4my+4=0的△=16m2-16>0,解得m<-1,或m>1,
且y1+y2=4m,y1•y2=4,
则x1+x2=m(y1+y2)-2=4m2-2,x1•x2=m2y1y2-m(y1+y2)+1=1,
∵
| AF |
| CF |
∴
| AF |
| CF |
即4m2-8=0,解得m=±
| 2 |
故直线l的方程为x+1=±
| 2 |
| 2 |
点评:本题考查的知识点是抛物线的简单性质,向量的数量积,直线与抛物线的综合应用,难度中档.

练习册系列答案
相关题目
已知函数f(x)=
g(x)=
,则函数f[g(x)]的所有零点之和是( )
|
|
A、-
| ||||
B、
| ||||
C、-1+
| ||||
D、1+
|