题目内容
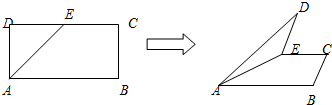
如图，在矩形ABCD中，AB=4，BC=3，E为DC边的中点，沿AE将AD折起，使二面角D-AE-B为60°，则异面直线BC与AD所成的角余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：异面直线及其所成的角
专题：
分析：如图所示，求出DG、AG、FH、DG、HF、HE的值，根据
•
=（
+
）•（
+
），利用两个向量的数量积的定义，求出异面直线BC与AD所成的角余弦值．
| AD |
| BC |
| AG |
| GD |
| FH |
| HE |
解答：
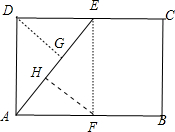解：如图所示：取AB的中点F，连接EF，则EF平行且等于BC．
作DG⊥AE，G为垂足，G∈AE，则DG=
=
，
AG=
=
，
=
+
．
作FH⊥AE，H为垂足，H∈AE，则FH=
=
，
EH=
=
，
=
=
+
．
∴
•
=（
+
）•（
+
）=
•
+
•
+
•
+
•
．
由二面角D-AE-B为60°，以及作图过程可得，
⊥
，
和
方向相同，
和
的夹角为120°，
⊥
，
设面直线BC与AD所成的角为θ，则3×3×cosθ=0+
•
+
•
cos120°+0，
求得cosθ=
，即异面直线BC与AD所成的角余弦值为
．
解：如图所示：取AB的中点F，连接EF，则EF平行且等于BC．作DG⊥AE，G为垂足，G∈AE，则DG=
| DA•DE |
| AE |
| 6 | ||
|
AG=
| AD2-DG2 |
| 9 | ||
|
| AD |
| AG |
| GD |
作FH⊥AE，H为垂足，H∈AE，则FH=
| FE•FA |
| AE |
| 6 | ||
|
EH=
| EF2-FH2 |
| 9 | ||
|
| BC |
| FE |
| FH |
| HE |
∴
| AD |
| BC |
| AG |
| GD |
| FH |
| HE |
| AG |
| FH |
| AG |
| HE |
| GD |
| FH |
| GD |
| HE |
由二面角D-AE-B为60°，以及作图过程可得，
| AG |
| FH |
| AG |
| HE |
| GD |
| FH |
| GD |
| HE |
设面直线BC与AD所成的角为θ，则3×3×cosθ=0+
| 9 | ||
|
| 9 | ||
|
| 6 | ||
|
| 6 | ||
|
求得cosθ=
| 7 |
| 13 |
| 7 |
| 13 |
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，用向量表示二面角的平面角，属于中档题．
练习册系列答案
相关题目
若A={y|y=2x，x∈R}，B{（x，y）|y=x2，x∈R}，则A∩B的子集个数为（ ）
| A、4 | B、2 | C、1 | D、0 |
若偶函数f（x）在（0，+∞）上单调递增，则不等式f（x2-3）＜f（2x）的解集为（ ）
| A、（1，3） |
| B、（-3，-1） |
| C、（-3，-1）∪（1，3） |
| D、（-1，1）∪（3，+∞） |
如图，在四棱锥V-ABCD中，四边形ABCD的对角线AC，BD相交于点O，已知底面ABCD是边长为2的正方形，其它四个侧面都是侧棱长为