题目内容
15.如图,在平行四边形ABCD中,E为DC边的中点,且$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=b,求$\overrightarrow{BE}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).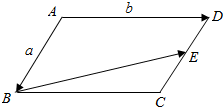
分析 根据向量的基本定理结合向量的加法和减法法则进行求解即可.
解答 解:$\overrightarrow{BE}$=$\overrightarrow{BC}$+$\overrightarrow{CE}$=$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{CD}$=$\overrightarrow{BC}$$+\frac{1}{2}\overrightarrow{BA}$=$\overrightarrow{AD}$-$\frac{1}{2}\overrightarrow{AB}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$,
故$\overrightarrow{BE}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
点评 本题主要考查向量的基本定理的应用,根据向量加减法的运算法则结合平行四边形的性质是解决本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
6.已知A,B均为锐角,sinA=$\frac{{\sqrt{5}}}{5}$,sinB=$\frac{{\sqrt{10}}}{10}$,则A+B的值为( )
| A. | $\frac{7π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
4.点M的极坐标是$(2,\frac{2π}{3})$,则点M直角坐标是( )
| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{3},1)$ | C. | $(-1,\sqrt{3})$ | D. | $(\sqrt{3},-1)$ |