Question

如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=l，E是PD的中点．
（1）求AB与平面AEC所成角的正弦值；
（2）若点F在线段PD上，二面角E-AC-F所成的角为θ，且tanθ=

2

2

，求

PF

FD

的值．

Answer 1

考点：用空间向量求平面间的夹角,用空间向量求直线与平面的夹角

专题：空间向量及应用

分析：（1）建立空间直角坐标系O-xyz，平面AEC的一个法向量

n

=（x，y，z），利用向量垂直的性质求出一个法向量，利用法向量与AB的夹角解答；
（2）设

PF

=λ

FD

，），

AF

=（0，

λ

1+λ

，

2

1+λ

），平面AFC的一个法向量为

m

=（a，b，c），利用法向量与平面内向量的垂直关系，得到关于λ的等式解之．

解答： 解：（1）如图建立空间直角坐标系O-xyz，如图

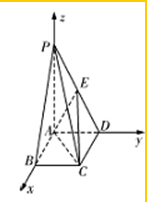
则A（0，0，0），B（2，0，0），C（2，1，0），E（0，

1

2

，1），

AC

=（2，1，0），

AE

=（0，

1

2

，1），

AB

=（2，0，0），
设AB与平面AEC所成的角为α，平面AEC的一个法向量

n

=（x，y，z），
则

n • AC =0 n • AE =0

，所以

2x+y=0 1 2 y+z=0

，取y=-2，

n

=（1，-2，1），
sinα=|cos＜

AB

，

n

＞|=

|2+0+0|

2 6

=

6

6

；
（2）设

PF

=λ

FD

，则F（0，

λ

1+λ

，

2

1+λ

），

AF

=（0，

λ

1+λ

，

2

1+λ

），
令平面AFC的一个法向量为

m

=（a，b，c），
则

m • AC =0 m • AF =0

，即

2a+b=0 bλ 1+λ + 2c 1+λ =0

，取b=-2，得

m

=（1，-2，λ），
由tanθ=

2

2

得cosθ=

6

3

=|cos＜

n

，

m

＞|=

|5+λ|

6 5+λ2

，
所以3λ²-10λ-5=0，所以λ=

5±2 10

3

，
又λ＞0，所以λ=

5+2 10

3

，即

PF

FD

=

5+2 10

3

．

点评：本题考查了空间向量的运用解答线面角和面面角的有关问题，关键是适当的建立坐标系，正确写出所需向量的坐标，利用线面角、面面角的三角函数与平面的法向量夹角的关系解答，属于中档题．