题目内容
已知圆C1:x2+(y-2)2=1,点Q(0,-1),动点M到圆C1的切线长与MQ的绝对值的比值为λ(λ>0).
(1)当λ=1和λ=
时,求出点M的轨迹方程;
(2)记λ=
时的点M的轨迹为曲线C2.若直线l1,l2的斜率均存在且垂直相交于点P,当l1,l2与曲线C1,C2相交,且恒有l1和l2被曲线C2截得的弦长相等,试求出所有满足条件的点P的坐标.
(1)当λ=1和λ=
| 10 |
(2)记λ=
| 10 |
考点:直线与圆锥曲线的关系
专题:计算题,直线与圆
分析:(1)设点M的坐标为(x,y),欲求动点M的轨迹方程,即寻找x,y间的关系式,结合题中条件列式化简即可得,求出当λ=1和λ=
时的方程即可;
(2)设P(m,n),l1:y-n=k(x-m),l2:y-n=-
(x-m),由于恒有l1和l2被曲线C2截得的弦长相等,则圆心(0,-
)到l1和l2的距离相等,运用点到直线的距离公式,化简整理,再由k为任意的得到m,n的方程,解得即可得到P的坐标.
| 10 |
(2)设P(m,n),l1:y-n=k(x-m),l2:y-n=-
| 1 |
| k |
| 4 |
| 3 |
解答:
解:(1)设M(x,y),则由题意可得,
:
=λ,
平方可得,(λ2-1)x2+(λ2-1)y2+(2λ2+4)y+λ2-3=0,
当λ=1时,点M的轨迹方程为:3y-1=0;
λ=
时,点M的轨迹方程为:圆9x2+9y2+24y+7=0;
(2)设P(m,n),l1:y-n=k(x-m),l2:y-n=-
(x-m),
由于恒有l1和l2被曲线C2截得的弦长相等,则圆心(0,-
)到l1和l2的距离相等,
即有
=
,化简可得,|
+n-km|=|
k+nk+m|,
即有
+n-km=
k+nk+m,或
+n-km+
k+nk+m=0,
则有(
+n-m)=k(
+n+m),或(
+n+m)=k(
+n-m),
则有由于k为任意的,则
+n-m=
+n+m=0,
解得,m=0,n=-
.
即有P(0,-
),检验满足条件.
故所有满足条件的点P的坐标为(0,-
).
| x2+(y-2)2-1 |
| x2+(y+1)2 |
平方可得,(λ2-1)x2+(λ2-1)y2+(2λ2+4)y+λ2-3=0,
当λ=1时,点M的轨迹方程为:3y-1=0;
λ=
| 10 |
(2)设P(m,n),l1:y-n=k(x-m),l2:y-n=-
| 1 |
| k |
由于恒有l1和l2被曲线C2截得的弦长相等,则圆心(0,-
| 4 |
| 3 |
即有
|
| ||
|
|
| ||||
|
| 4 |
| 3 |
| 4 |
| 3 |
即有
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
则有(
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
则有由于k为任意的,则
| 4 |
| 3 |
| 4 |
| 3 |
解得,m=0,n=-
| 4 |
| 3 |
即有P(0,-
| 4 |
| 3 |
故所有满足条件的点P的坐标为(0,-
| 4 |
| 3 |
点评:本题考查轨迹方程的求法,考查直线和圆相切的切线长问题和直线和圆相交的弦长问题,考查运算能力,属于中档题.

练习册系列答案
相关题目
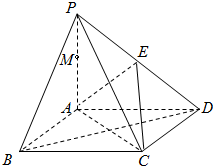 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4 如图,长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高为1,M为线段AB的中点,则三棱锥C-MC1D1的体积为( )
如图,长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高为1,M为线段AB的中点,则三棱锥C-MC1D1的体积为( )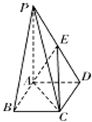 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=l,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=l,E是PD的中点.