题目内容
【题目】如图,在三棱锥P﹣ABC中,PA=PC=5,PB=4,AB=BC=2 ![]() ,∠ACB=30°.
,∠ACB=30°. 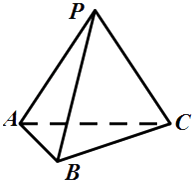
(1)求证:AC⊥PB;
(2)求三棱锥P﹣ABC的体积.
【答案】
(1)证明:取AC的中点D,连接PD、BD.
∵AB=BC,PA=AC,D为AC的中点,
∴PD⊥AC,BD⊥AC,
又BD平面PBD,PD平面PBD,BD∩PD=D,
∴AC⊥平面PBD.
∵PB平面PBD,
∴AC⊥PB.
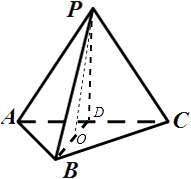
(2)解:AB=BC=2 ![]() ,∠ACB=30°.
,∠ACB=30°.
∴BD= ![]() BC=
BC= ![]() ,AD=CD=
,AD=CD= ![]() AC=3.
AC=3.
∴PD= ![]() =4,又PB=4,
=4,又PB=4,
∴△PBD是等腰三角形,作PB⊥BD于O,则O为BD的中点,
∴PO= ![]() =
= ![]() .
.
∴S△PBD= ![]() =
= ![]() =
= ![]() .
.
∴VP﹣ABC=VA﹣PBD+VC﹣PBD= ![]() S△PBD(AD+CD)=
S△PBD(AD+CD)= ![]() =
= ![]() .
.
【解析】(1)取AC的中点D,连接PD、BD,利用三线合一得出PD⊥AC,BD⊥AC,于是AC⊥平面PBD,从而得出AC⊥PB;(2)计算AC,PD从而得出PB=PD,求出△PBD的面积,则VP﹣ABC= ![]() S△PBDAC.
S△PBDAC.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的60名候车的乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示:
组别 | 一 | 二 | 三 | 四 | 五 |
候车时间(分钟) |
|
|
|
|
|
人数 | 2 | 6 | 4 | 2 | 1 |
(1)估计这15名乘客的平均候车时间;
(2)估计这60 名乘客中候车时间少于10 分钟的人数;
(3)若从上表第三、四组的6人中选2人作进一步的问卷调查,求抽到的2人恰好来自不同组的概率.
【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 2 | 4 | 8 | 4 | 2 |
男生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 1 | 5 | 6 | 5 | 3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
男生 | |||
女生 | |||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)