Question

【题目】已知，若关于的方程恰好有 4 个不相等的实数解，则实数的取值范围为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】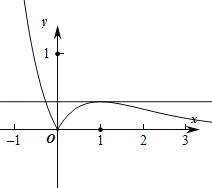

化简可得f（x）==

当x≥0时，f′（x）=，

当0≤x＜1时，f′（x）＞0，当x≥1时，f′（x）≤0

∴f（x）在（0，1）上单调递增，在（1，+∞）单调递减；

当x＜0时，f′（x）=＜0，f（x）为减函数，

∴函数f（x）=在（0，+∞）上有一个最大值为f（1）=，作出函数f（x）的草图如图：

设m=f（x），当m＞时，方程m=f（x）有1个解，

当m=时，方程m=f（x）有2个解，

当0＜m＜时，方程m=f（x）有3个解，

当m=0时，方程m=f（x），有1个解，

当m＜0时，方程m=f（x）有0个解，

则方程f2（x）﹣tf（x）+t﹣1=0等价为m2﹣tm+t﹣1=0，

要使关于x的方程f2（x）﹣tf（x）+t﹣1=0恰好有4个不相等的实数根，

等价为方程m2﹣tm+t﹣1=0有两个不同的根m1＞且0＜m2＜，

设g（m）=m2﹣tm+t﹣1，

则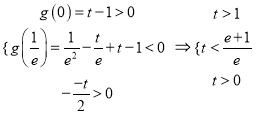

解得1＜t＜1+，

故答案选：C。