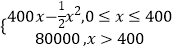题目内容
【题目】已知函数f(x)= ![]() .(x>0)
.(x>0)
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)若当x>0时,f(x)> ![]() 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
【答案】
(1)解:函数f(x)= ![]()
∴f′(x)= ![]() [
[ ![]() ﹣1﹣ln(x+1)]=﹣
﹣1﹣ln(x+1)]=﹣ ![]() [
[ ![]() +ln(x+1)].
+ln(x+1)].
由x>0,x2>0, ![]() >0,ln(x+1)>0,得f′(x)<0.
>0,ln(x+1)>0,得f′(x)<0.
因此函数f(x)在区间(0,+∞)上是减函数
(2)解:解法一:当x>0时,f(x)> ![]() 恒成立,令x=1有k<2[1+ln2].
恒成立,令x=1有k<2[1+ln2].
又k为正整数.则k的最大值不大于3.
下面证明当k=3时,f(x)> ![]() (x>0)恒成立.
(x>0)恒成立.
即证明x>0时(x+1)ln(x+1)+1﹣2x>0恒成立.
令g(x)=(x+1)ln(x+1)+1﹣2x,
则g′(x)=ln(x+1)﹣1.
当x>e﹣1时,g′(x)>0;当0<x<e﹣1时,g′(x)<0.
∴当x=e﹣1时,g(x)取得最小值g(e﹣1)=3﹣e>0.
∴当x>0时,(x+1)ln(x+1)+1﹣2x>0恒成立.
因此正整数k的最大值为3.
解法二:当x>0时,f(x)> ![]() 恒成立.
恒成立.
即h(x)= ![]() >k对x>0恒成立.
>k对x>0恒成立.
即h(x)(x>0)的最小值大于k.
由h′(x)= ![]() ,记Φ(x)=x﹣1﹣ln(x+1).(x>0)
,记Φ(x)=x﹣1﹣ln(x+1).(x>0)
则Φ′(x)= ![]() >0,
>0,
∴Φ(x)在(0,+∞)上连续递增.
又Φ(2)=1﹣ln3<0,Φ(3)=2﹣2ln2>0,
∴Φ(x)=0存在惟一实根a,且满足:a∈(2,3),a=1+ln(a+1),
由x>a时,Φ(x)>0,h′(x)>0;0<x<a时,Φ(x)<0,h′(x)<0知:
h(x)(x>0)的最小值为h(a)= ![]() =a+1∈(3,4).
=a+1∈(3,4).
因此正整数k的最大值为3
【解析】(1)直接求函数f(x)的导函数,化简导函数分子,判断正负即可;(2)可以先利用特殊值x=1先尝试k的可能值,然后用导数的方法予以证明;或者构造新函数将问题转化为求函数最值,利用函数的导数去研究函数的最值即可.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.