题目内容
【题目】已知函数![]() 在
在![]() 上有最大值1和最小值0,设
上有最大值1和最小值0,设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() (
(![]() 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的值分别为1、0.(2)
的值分别为1、0.(2) ![]() .(3)
.(3) ![]() .
.
【解析】试题分析:
(1)由题意得到关于实数m,n的方程组,求解方程组可得![]() 的值分别为1、0.
的值分别为1、0.
(2)由题意换元,令![]() ,结合换元之后的不等式的解集可得实数
,结合换元之后的不等式的解集可得实数![]() 的取值范围是
的取值范围是![]() .
.
(3) 记![]() ,原问题等价于
,原问题等价于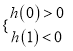 ,求解不等式组可得实数
,求解不等式组可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 上是增函数,∴
上是增函数,∴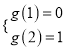 ,
,
即![]() ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() ,无最大值和最小值;
,无最大值和最小值;
当![]() 时,
时, ![]() 在
在![]() 上是减函数,∴
上是减函数,∴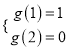 ,即
,即![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]() 舍去.
舍去.
综上, ![]() 的值分别为1、0.
的值分别为1、0.
(2)由(1)知![]() ,∴
,∴![]() 在
在![]() 上有解等价于
上有解等价于
![]() 在
在![]() 上有解,
上有解,
即![]() 在
在![]() 上有解,令
上有解,令![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,记
,记![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.
(3)原方程可化为![]() ,令
,令![]() ,则
,则![]() ,
,
由题意知![]() 有两个不同的实数解
有两个不同的实数解![]() ,
, ![]() ,
,
其中![]() ,
, ![]() 或
或![]() ,
, ![]() ,
,
记![]() ,则
,则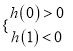 得
得![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目