题目内容
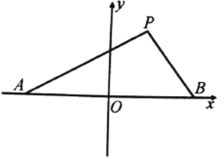
【题目】如图,已知椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,右焦点为
倍,右焦点为![]() ,点
,点![]() 分别是该椭圆的上、下顶点,点
分别是该椭圆的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴交点除外),直线
轴交点除外),直线![]() 交椭圆于另一点
交椭圆于另一点![]() ,记直线
,记直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]()

(1)当直线![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 的最小值.
的最小值.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用椭圆的标准方程得到基本量,写出点的坐标,写出直线![]() 的方程为
的方程为![]() ,即
,即![]() ,求出P,联立直线与椭圆求出M,计算向量的数量积;(2)设
,求出P,联立直线与椭圆求出M,计算向量的数量积;(2)设![]() ,且
,且![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() 联立直线与椭圆的方程,求出M的坐标,从而
联立直线与椭圆的方程,求出M的坐标,从而 ,然后利用均值不等式即可求出.
,然后利用均值不等式即可求出.
试题解析:
(1)由椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍得
倍得![]()
由题意![]() ,焦点
,焦点![]() ,当直线
,当直线![]() 过点
过点![]() 时,则直线
时,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,令
,令![]() 得
得![]() ,则
,则![]()
联立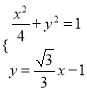 ,解得
,解得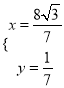 ,或
,或![]() (舍),即
(舍),即
因为
所以![]()
(2)设![]() ,且
,且![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]()
则直线![]() 的方程为
的方程为![]()
联立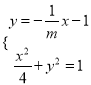 ,化简得
,化简得![]() ,解得
,解得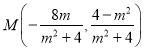 ,
,
所以 ,
,
则![]()
所以![]() 的最小值为
的最小值为![]()

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
Ⅰ.请完成上面的列联表;
Ⅱ.根据列联表的数据,是否有![]() 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.
参考公式与临界值表:![]() .
.

【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子发芽数,得到如下资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1组与第5组的两组数据,请根据第2组至第4组的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: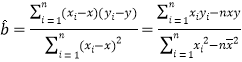 ,
,![]() )
)
【题目】某市2010年至2016年新开楼盘的平均销售价格![]() (单位:千元/平米)的统计数据如下表:
(单位:千元/平米)的统计数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 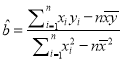 ,
, ![]() .
.