题目内容
【题目】已知四棱锥P-ABCD,底面ABCD是边长为2的蓌形,PA⊥平面ABCD,PA=2,∠ABC=60°,E,F分别是BC,PC的中点。
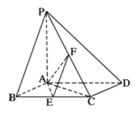
(1)求证:AE⊥PD;
(2)求二面角E-AF-C的余弦值。
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(Ⅰ)根据已知条件,容易得出AE⊥BC,AE⊥AD,而PA⊥平面ABCD,所以便可得到AE⊥平面PAD,所以得到AE⊥PD;(Ⅱ)根据(Ⅰ)可知AE,AD,PA三条直线两两垂直,所以可分别以这三条直线分别为x轴,y轴,z轴建立空间直角坐标系,然后分别设平面AEF,和平面ACF的法向量为![]()
![]() 可设菱形的边长为2,根据条件可求出向量
可设菱形的边长为2,根据条件可求出向量![]() 的坐标,根据法向量和这三个向量的垂直关系即可求出
的坐标,根据法向量和这三个向量的垂直关系即可求出![]() 的坐标,所以求这两个向量夹角的余弦值就可得到二面角E-AF-C的余弦值
的坐标,所以求这两个向量夹角的余弦值就可得到二面角E-AF-C的余弦值
试题解析:(Ⅰ)BC=AB,∠ABC=60°,∴AE⊥BC,∴△ABC是等边三角形;
又E是BC中点,∴AE⊥BC,BC∥AD,∴AE⊥AD;
PA⊥面ABCD,AE平面ABCD,PA⊥AE,即AE⊥PA,AD∩PA=A;
∴AE⊥平面PAD,∴AE⊥PD
(2)以菱形对角线交点为原点建立坐标系更好求点坐标(个人观点)

![]() =(
=(![]() ,0,0),
,0,0),![]() =(
=(![]() ,
,![]() ,1)
,1)
设平面AEF的一法向量为m=(x1,y1,z1),则 ,因此
,因此 取z1=-1,则m=(0,2,-1)分 因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故
取z1=-1,则m=(0,2,-1)分 因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故![]() 为平面AFC的一法向量.又
为平面AFC的一法向量.又![]() =(-
=(-![]() ,3,0),所以cos<m,
,3,0),所以cos<m,![]() >=
>= .因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
.因为二面角E-AF-C为锐角,所以所求二面角的余弦值为![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目