题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点, 极轴为
,以极点为原点, 极轴为![]() 轴的正半轴, 建立平面直角坐标系, 直线
轴的正半轴, 建立平面直角坐标系, 直线![]() 的参数方程为
的参数方程为![]() 为参数).
为参数).
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系, 并说明理由;
的位置关系, 并说明理由;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点, 且
两点, 且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)直线![]() 与曲线
与曲线![]() 相交;(2)
相交;(2)![]() .
.
【解析】
试题分析:(1)由![]()
![]()
![]()
![]()
![]()
![]()
![]() ,又直线
,又直线![]() 过点
过点![]() ,且该点到圆心的距离为
,且该点到圆心的距离为![]()
![]() 直线
直线![]() 与曲线
与曲线![]() 相交;(2)先当验证直线
相交;(2)先当验证直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 过不成立
过不成立![]() 直线
直线![]() 必有斜率, 设其方程为
必有斜率, 设其方程为
![]()
![]()
![]()
![]() 圆心到直线
圆心到直线![]() 的距离
的距离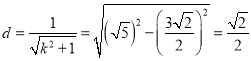
![]()
![]()
![]()
![]() 的斜率为
的斜率为![]() .
.
试题解析:(1)因为 ![]() ,所以
,所以![]() ,所以曲线
,所以曲线![]() 的直角坐标方程为
的直角坐标方程为
![]() ,即
,即![]() ,因为直线
,因为直线![]() 过点
过点![]() ,且该点到圆心的距离为
,且该点到圆心的距离为![]() ,所以直线
,所以直线![]() 与曲线
与曲线![]() 相交.
相交.
(2)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 过圆心
过圆心![]() ,则直线
,则直线![]() 必有斜率, 设其方程为
必有斜率, 设其方程为
![]() ,即
,即![]() ,圆心到直线
,圆心到直线![]() 的距离
的距离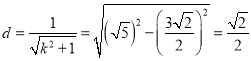 ,
,
解得![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目