题目内容
【题目】已知函数![]()
![]() ,
,
(1)若曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,求
,求![]() 的值;
的值;
(2)讨论函数![]() 的单调性;
的单调性;
(3)设函数![]() ,若至少存在一个
,若至少存在一个![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;
(2)当![]()
![]() 的单调增区间为
的单调增区间为![]() ,
,
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]()
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]() .
.
(3)![]()
【解析】
试题分析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,可得到
,可得到![]() 的值,可得
的值,可得![]() 的值;(2)
的值;(2)![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况讨论
三种情况讨论![]() 的单调性;(3)若至少存在一个
的单调性;(3)若至少存在一个![]() ,使得
,使得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴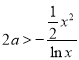 有解,令
有解,令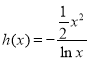 ,讨论函数
,讨论函数![]() 的性质,可得到
的性质,可得到
实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
∴![]() ,
,![]()
解得![]() ,∴
,∴![]() .
.
(2)![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]()
当![]() 时,由
时,由![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() .
.
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() .
.
综上所述:当![]() 时,
时, ![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]()
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]() .
.
(3)若至少存在一个![]() ,使得
,使得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴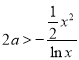 有解,令
有解,令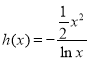 ,
,
∴![]()
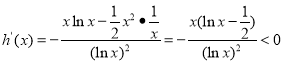 ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,![]()
∴![]() 得,
得,![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”、“演讲社”三个金牌社团中抽6人组成社团管理小组,有关数据见下表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求![]() 的值;
的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.