题目内容
【题目】设数列![]() 满足
满足![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]() .
.
【答案】(1) ![]() ,
, ![]() ;(2)
;(2) ![]() ;(3) 见解析;
;(3) 见解析;
【解析】试题分析:(1)由![]() 可得
可得![]() ,所以
,所以![]() 是首项为
是首项为![]() ,公比为3的等比数列,进而可求得
,公比为3的等比数列,进而可求得![]()
(2)由题可转化为 ,即
,即![]() ,对任意
,对任意![]() 恒成立,再看成关于m的一次函数,需
恒成立,再看成关于m的一次函数,需![]() ,解得
,解得
![]() 的取值范围为
的取值范围为![]() .
.
(3)由(1)知![]() ,利用当
,利用当![]() 时,
时, ![]() ,对
,对![]() 进行放缩可得
进行放缩可得
![]() .
.
试题解析:(1)解:由![]() (
(![]() 且
且![]() )得
)得![]() (
(![]() 且
且![]() )
)
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,(
,(![]() 且
且![]() )
)
∴![]() 是首项为3,公比为3的等比数列.
是首项为3,公比为3的等比数列.
∴![]() .
.
∴![]() ,
, ![]() .
.
(2)要使对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,
恒成立,
则须使 ,
,
即![]() ,对任意
,对任意![]() 恒成立,
恒成立,
∴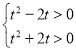 ,解得
,解得![]() 或
或![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.
(3)证明:由(1)知![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() ,
,
所以![]() .
.

练习册系列答案
相关题目