Question

【题目】已知椭圆的离心率为,过右焦点作垂直于椭圆长轴的直线交椭圆于两点，且为坐标原点.

(1)求椭圆的方程；

(2) 设直线与椭圆相交于两点,若.

①求的值；

②求的面积的最小值.

Answer 1

【答案】（1）；（2）①，②.

【解析】

（1）利用椭圆的离心率公式，通径的长和椭圆中a，b，c的关系，求得a，b，c的值，进而可得椭圆的方程.

(2)①通过联立直线和椭圆方程，得到关于x的一元二次方程，利用一元二次方程的根与系数的关系，求出，再结合向量表示垂直得，进而求解；

②设直线OA的斜率为.分和两种情况讨论，当时，通过联立直线与椭圆方程和三角形面积公式，将面积的最小值问题转化为求函数的最值问题求解，再结合时的情况，得面积的取值范围，进而求得最小值.

(1) 已知椭圆的离心率为，可知 ，

根据椭圆的通径长为 ，结合椭圆中 ，

可解得 ，

故椭圆C的方程为 .

（2）①已知直线AB的方程为 , 设

与椭圆方程联立有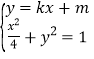,消去y,得 ,

所以 ，

因 ,所以 ，即 ，

所以 .整理得 ,

所以为

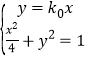②设直线OA的斜率为.当时,则的方程OA为,OB的方程为 ，联立得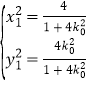,同理可求得 ,

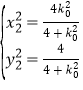故△AOB的面积为 .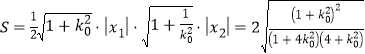

令 ，则

令 ,所以 .

所以 ，当时,可求得S=1,故,故S的最小值为