题目内容
【题目】以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是ρ=2,矩形ABCD内接于曲线C1 , A,B两点的极坐标分别为(2, ![]() )和(2,
)和(2, ![]() ),将曲线C1上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线C2 .
),将曲线C1上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线C2 .
(1)写出C,D的直角坐标及曲线C2的参数方程;
(2)设M为C2上任意一点,求|MA|2+|MB|2+|MC|2+|MD|2的取值范围.
【答案】
(1)解:曲线C1的极坐标方程是ρ=2,矩形ABCD内接于曲线C1,A,B两点的极坐标分别为(2, ![]() )和(2,
)和(2, ![]() ),利用对称性可得:C
),利用对称性可得:C ![]() ,D
,D ![]() ,分别化为直角坐标:C
,分别化为直角坐标:C ![]() ,D
,D ![]() .
.
曲线C1的极坐标方程是ρ=2,化为直角坐标方程:x2+y2=4.
设曲线C2.上的任意一点坐标P(x,y),曲线C1的任意一点P′(x′,y′),则 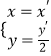 ,可得
,可得 ![]() .代入(x′)2+(y′)2=4,得x2+4y2=4,其参数方程为:
.代入(x′)2+(y′)2=4,得x2+4y2=4,其参数方程为: ![]()
(2)解:A ![]() ,B
,B ![]() .设M(2cosθ,sinθ).
.设M(2cosθ,sinθ).
|MA|2+|MB|2+|MC|2+|MD|2= ![]() +
+ ![]() +(sinθ﹣1)2+
+(sinθ﹣1)2+ ![]() +(sinθ+1)2+
+(sinθ+1)2+ ![]() +(sinθ+1)2
+(sinθ+1)2
=12cos2θ+20∈[20,32]
【解析】(1)利用对称性可得:C ![]() ,D
,D ![]() ,分别化为直角坐标.曲线C1的极坐标方程是ρ=2,利用互化公式可得直角坐标方程.设曲线C2 . 上的任意一点坐标P(x,y),曲线C1的任意一点P′(x′,y′),则
,分别化为直角坐标.曲线C1的极坐标方程是ρ=2,利用互化公式可得直角坐标方程.设曲线C2 . 上的任意一点坐标P(x,y),曲线C1的任意一点P′(x′,y′),则 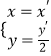 ,可得
,可得 ![]() .代入圆的方程可得x2+4y2=4,可得参数方程.(2)A
.代入圆的方程可得x2+4y2=4,可得参数方程.(2)A ![]() ,B
,B ![]() .设M(2cosθ,sinθ).利用两点之间的距离公式、三角函数的基本关系式及其值域即可得出.
.设M(2cosθ,sinθ).利用两点之间的距离公式、三角函数的基本关系式及其值域即可得出.

练习册系列答案
相关题目