题目内容
【题目】已知四棱锥P﹣ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,AB=2CD=2 ![]() ,E,F分别是AB,AP的中点.
,E,F分别是AB,AP的中点. 
(1)求证:AC⊥EF;
(2)求二面角F﹣OE﹣A的余弦值.
【答案】
(1)证明:由ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,可知:△OAB是等腰直角三角形,
∵AB=2CD=2 ![]() ,E是AB的中点,∴OE=EA=EB=
,E是AB的中点,∴OE=EA=EB= ![]() ,可得OA=OB=2.
,可得OA=OB=2.
∵PO⊥底面ABCD,∴PO⊥OA,PO⊥OB.又OA⊥OB.
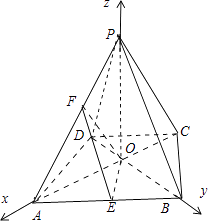
∴可以建立如图所示的空间直角坐标系.
则O(0,0,0),A(2,0,0),B(0,2,0),P(0,0,2),E(1,1,0),F(1,0,1).
∴ ![]() ,
, ![]() .
.
∴ ![]() ,∴EF⊥AO,即EF⊥AC
,∴EF⊥AO,即EF⊥AC
(2)解:由(1)可知: ![]() ,
, ![]() .
.
设平面OEF的法向量为 ![]() ,
,
则 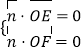 ,得
,得 ![]() ,令x=1,则y=z=﹣1.
,令x=1,则y=z=﹣1.
∴ ![]() .
.
∵PO⊥平面OAE,∴可取 ![]() 作为平面OAE的法向量.
作为平面OAE的法向量.
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
由图可知:二面角F﹣OE﹣A的平面角是锐角θ.
因此, ![]() .
.
【解析】(1)通过建立空间直角坐标系,利用EF与AO的方向向量的数量积等于0,即可证明垂直;(2)利用两个平面的法向量的夹角即可得到二面角的余弦值.

练习册系列答案
相关题目
