题目内容
【题目】已知两点
，点P是椭圆
上任意一点，则点P到直线AB的距离最大值为（ ）
A. 
B. 
C. 6D. 
【答案】B
【解析】
先求出直线AB的方程，然后结合图形，将点到直线的的最大距离转化为求与直线AB平行且与椭圆相切的直线与直线AB的最大距离，再利用两平行线间的距离求出即可
由两点A（-1，0），B（0，1），则直线AB的方程为y=x+1，
由图可知，直线y=x+m（m＜0）和椭圆相切于P点时，到AB的距离最大．
联立方程得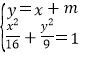
， 整理得25x2+32mx+16m2-144=0
由于直线y=x+m和椭圆相切，则△=（32m）2-4×25×（16m2-144）=0，解得m= -5或m=5（舍去）
由于y=x+1与直线y=x-5的距离为
则点P到直线AB距离的最大值为
，
故选B.
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】本市某玩具生产公司根据市场调查分析，决定调整产品生产方案，准备每天生产
， 
， 
三种玩具共100个，且
种玩具至少生产20个，每天生产时间不超过10小时，已知生产这些玩具每个所需工时（分钟）和所获利润如表：
玩具名称 |
|
|
|
工时（分钟） | 5 | 7 | 4 |
利润（元） | 5 | 6 | 3 |
（Ⅰ）用每天生产
种玩具个数
与
种玩具
表示每天的利润
（元）；
（Ⅱ）怎样分配生产任务才能使每天的利润最大，最大利润是多少？
