题目内容
1. 如图,已知抛物线y2=2px(p>0)的焦点F恰好是双曲线$\frac{x^2}{a^2}-\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线y2=2px(p>0)的焦点F恰好是双曲线$\frac{x^2}{a^2}-\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}+1$ | D. | $\sqrt{2}-1$ |
分析 根据抛物线和双曲线有相同的焦点求得p和c的关系,根据AF⊥x轴可判断出|AF|的值和A的坐标,代入双曲线方程与p=2c,b2=c2-a2联立求得a和c的关系式,然后求得离心率e.
解答 解:∵抛物线的焦点和双曲线的焦点相同,
∴p=2c
设A是它们的一个公共点,且AF垂直x轴,
设A点的纵坐标大于0,
∴|AF|=p,
∴A($\frac{p}{2}$,p),
∵点A在双曲线上,
∴$\frac{{p}^{2}}{4{a}^{2}}-\frac{{p}^{2}}{{b}^{2}}$=1,
∵p=2c,b2=c2-a2,
∴$\frac{{c}^{2}}{{a}^{2}}-\frac{4{c}^{2}}{{c}^{2}-{a}^{2}}$=1,
化简得:c4-6c2a2+a4=0,
∴e4-6e2+1=0,
∵e2>1,
∴e2=3+2$\sqrt{2}$
∴e=$\sqrt{2}$+1,
故选:C
点评 本题主要考查关于双曲线的离心率的问题,属于中档题,本题利用焦点三角形中的边角关系,得出a、c的关系,从而求出离心率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.cos$\frac{π}{12}$+$\sqrt{3}$sin$\frac{π}{12}$的值为( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
9.函数f(x)=-cosx•lg|x|的部分图象是( )
| A. | 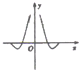 | B. | 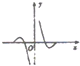 | C. | 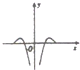 | D. | 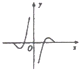 |