题目内容
9．函数f（x）=-cosx•lg|x|的部分图象是（ ）| A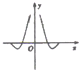． |  | B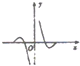． |  | C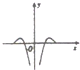． |  | D． |  |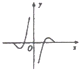
分析 根据函数的奇偶性排除BD，再根据x的变化趋势排除C．
解答 解：由于f（x）=-cosx•lg|x|，
∴f（-x）=-cos（-x）•lg|-x|=-cosx•lg|x|=f（x），
故函数f（x）是偶函数，排除B，D；
又当x→0时，lg|x|→-∞，cosx→1，
∴f（x）→+∞，故排除C，
故选：A．
点评 本题考查函数的图象，考查同学们对函数基础知识的把握程度以及数形结合的思维能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．设1，a+bi，b+ai是一等比数列的连续三项，则a，b的值分别为（ ）
| A． | a=±$\frac{\sqrt{3}}{2}$，b=±$\frac{1}{2}$ | B． | a=-$\frac{1}{2}$，b=$\frac{\sqrt{3}}{2}$ | C． | a=±$\frac{\sqrt{3}}{2}$，b=$\frac{1}{2}$ | D． | a=-$\frac{1}{2}$，b=-$\frac{\sqrt{3}}{2}$ |
17．已知函数f（x）=Asin（ωx+φ）（ω＞0），如果存在实数x1使得对任意的实数x，都有f（x1）≤f（x）≤
f（x1+2015）成立，则ω的最小值为（ ）
f（x1+2015）成立，则ω的最小值为（ ）
| A． | $\frac{π}{2015}$ | B． | $\frac{1}{2015}$ | C． | $\frac{π}{4010}$ | D． | $\frac{1}{4010}$ |
4．在△ABC中，角A，B，C的对边分别为a，b，c，若a2-b2-c2=-$\sqrt{3}$bc，则A等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
1．
如图，已知抛物线y2=2px（p＞0）的焦点F恰好是双曲线$\frac{x^2}{a^2}-\frac{{y{\;}^2}}{b^2}$=1的右焦点，且两条曲线的交点的连线过F，则该双曲线的离心率为（ ）
如图，已知抛物线y2=2px（p＞0）的焦点F恰好是双曲线$\frac{x^2}{a^2}-\frac{{y{\;}^2}}{b^2}$=1的右焦点，且两条曲线的交点的连线过F，则该双曲线的离心率为（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{2}+1$ | D． | $\sqrt{2}-1$ |