题目内容
16.设数列{an}是公差为d的等差数列,且a5=6.(1)若d∈N*,其数列{an}中任意连续两项的和仍为数列{an}中的项,求d的值;
(2)若a3>1,且自然数n1,n2,…,nt,…(t∈N*)满足5<n1<n2<…<n2<…,使得a3,a5,an1,…,ant,…成等比数列,求a3的所有可能值.
分析 (1)求出数列的通项公式,假设任意连续两项的和an+an+1,进行比较即可得到结论.
(2)因为数列{an}是一个公差不为零的等差数列,且a5=6,所以am=a3+(mt-3)×$\frac{6-a3}{2}$( mt>5,mt∈N*),又am=a3($\frac{6}{a3}$)t+1,由此能够求出a3的一切可能值.
解答 解:(1)a5=6,
an=a5+d(n-5)=6+d(n-5)
任意连续两项的和an+an+1=12+d(n-5+n+1-5)=12+d(2n-11)
因为数列{an}中任意连续两项的和仍为数列{an}中的项,
所以an+an+1=12+d(2n-11)=6+d(m-5),
即6+d(2n-11-m+5)=6+d(2n-m-6)=0,
则m=$\frac{6}{d}$+2n-6,
则因此d须为6的因数,因此只可能有d=1,2,3,6
但同时须有$\frac{6}{d}$+2n-6>0,
若d=1,则不等式等价为6+2n-6=2n>0,成立,
若d=2,则不等式等价为3+2n-6=2n-3>0,当n=1时不成立,
若d=3,则不等式等价为2+2n-6=2n-4>0,当n=1,2时不成立,
若d=6,则不等式等价为1+2n-6=2n-5>0,当n=1,2时不成立,
因此只能取d=1.
(2)因为数列{an}是一个公差不为零的等差数列,且a5=6,
所以an=a3+(nt-3)×$\frac{6-a3}{2}$( nt>5,nt∈N*)
又an=a3($\frac{6}{a3}$)t+1,
故a3($\frac{6}{a3}$)t+1=a3+(nt-3)×$\frac{6-a3}{2}$,
即$\frac{6t+1-a3t+1}{a3t}$=(nt-3)×$\frac{6-a3}{2}$,
故$\frac{(6-a3)(6t+6t-1a3+…+6a3t-1+a3t)}{a3t}$=(nt-3)×$\frac{6-a3}{2}$.
由a3≠a5,所以a3≠6.
nt=5+2[($\frac{6}{a3}$)t+($\frac{6}{a3}$)t-1+…+($\frac{6}{a3}$)],t∈N*.
当t=1时,n1=5+2×$\frac{6}{a3}$=5+$\frac{12}{a3}$.
由n1∈N*,且a3>1,
则$\frac{12}{a3}$=1,2,3,4,5,6,7,8,9,10,11.
当t=2时,m2=5+2×[($\frac{6}{a3}$)2+$\frac{6}{a3}$],
所以$\frac{12}{a3}$为奇数时,n2不为整数,不符合.
所以,$\frac{12}{a3}$=2,4,6,8,10.从而a3=6,3,2,$\frac{3}{2}$,$\frac{6}{5}$,
又因为数列{an}是一个公差不为零的等差数列,且a3≠6.
所以a3=3,2,$\frac{3}{2}$,$\frac{6}{5}$.经检验均满足题意.
点评 本题考查数列与不等式的综合运用,综合性强,难度大,对数学思维能力要求较高.解题时认真审题,仔细解答.

 优学名师名题系列答案
优学名师名题系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | (0,1) | B. | (-1,3) | C. | (1,1) | D. | (-1,1) |
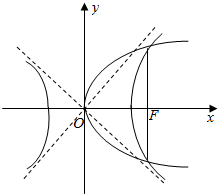 如图,已知抛物线y2=2px(p>0)的焦点F恰好是双曲线$\frac{x^2}{a^2}-\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线y2=2px(p>0)的焦点F恰好是双曲线$\frac{x^2}{a^2}-\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}+1$ | D. | $\sqrt{2}-1$ |