题目内容
17.若实数x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ y≥-1\\ x+y≤1\end{array}\right.$,则z=2x-y的最大值为( )| A. | -1 | B. | $\frac{1}{2}$ | C. | 5 | D. | 7 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.
解答 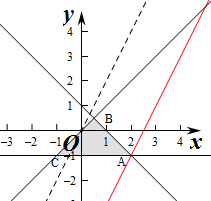 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=2x-y得y=2x-z,
平移直线y=2x-z,
由图象可知当直线y=2x-z经过点A时,直线y=2x-z的截距最小,
此时z最大.
由$\left\{\begin{array}{l}{y=-1}\\{x+y=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,即A(2,-1)
代入目标函数z=2x-y,
得z=4-(-1)=5.
即z=2x-y的最大值为5,
故选:C.
点评 本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.为了了解城市人均GDP与人均日产生活垃圾量之间的相关关系,国家统计局与卫生管理局随机抽查了6个城市,具体数据如表
(1)计算这6个城市人均日产生活垃圾量的平均值(单位:千克);
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
| 城市 | 天津 | 重庆 | 广州 | 深圳 | 武汉 | 西安 |
| 人均GDP(万美元)x | 1.64 | 0.69 | 1.93 | 2.22 | 1.43 | 0.92 |
| 人均日产生活垃圾量(千克)y | 0.64 | 0.51 | 1.05 | 1.15 | 0.99 | 0.76 |
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
9.下面关于算法的说法正确的是( )
| A. | 秦九韶算法是求两个数的最大公约数的方法 | |
| B. | 更相减损术是求多项式的值的方法 | |
| C. | 割圆术是采用正多边形面积逐渐逼近圆面积的算法计算圆周率π | |
| D. | 以上结论皆错 |
6.已知f′(x)是奇函数f(x)的导函数,f(-1)=0,当x>0时,xf′(x)+f(x)>0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
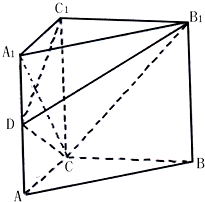 某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.
某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.