题目内容

5．为了了解城市人均GDP与人均日产生活垃圾量之间的相关关系，国家统计局与卫生管理局随机抽查了6个城市，具体数据如表
城市天津重庆广州深圳武汉西安
人均GDP（万美元）x1.640.691.932.221.430.92
人均日产生活垃圾量（千克）y0.640.511.051.150.990.76
（1）计算这6个城市人均日产生活垃圾量的平均值（单位：千克）；
（2）求出x与y之间的线性回归方程；
（提供下列参考数据：$\sum_{i=1}^6{x_i}=8.82$，$\sum_{i=1}^6{x_i}{y_i}=8.1$，$\sum_{i=1}^6{x_i}^2=14.7$）
（3）如果某城市的人均GDP达到了3万美元，预测该城市的人均日产生活垃圾量为多少千克？

分析 （1）直接利用已知条件求解平均值即可．
（2）利用已知条件求解回归直线方程即可．
（3），通过回归直线方程求解该城市的人均日产生活垃圾量．

解答 （本小题满分14分）
（1）解：6个城市人均日产生活垃圾量的均值为$\overline y=0.85$千克…（3分）
（2）解：根据提供的数据有 $\overline x=1.47$，$\sum_{i=1}^6{{x_i}{y_i}}=8.1，\sum_{i=1}^6{x_i^2}=14.7$
由公式$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{（\overline x）}^2}}}}=\frac{8.10-6×1.47×0.85}{{14.71-6×{{1.47}^2}}}=\frac{8.1-7.50}{14.71-12.96}=\frac{0.6}{1.75}=\frac{12}{35}≈0.343$
又0.85=0.343×1.47+a⇒a=0.35，∴线性回归方程为$\hat y=0.343x+0.35$…（11分）
（3）解：如果x=3时，$\hat y=0.343×3+0.35=1.379$千克，则该城市的人均日产垃圾量为1.379千克…（14分）

点评 本题考查回归直线方程的求法与应用，基本知识的考查．

练习册系列答案
相关题目
15．已知三角形的三个顶点 A（-4，0），B（2，-4），C（0，2）．
（1）求BC边上中线所在直线的方程（要求写成系数为整数的一般式方程）；
（2）求△ABC的面积S．
16．已知圆O：x2+y2=4，直线l：y=kx-4．
（1）若直线l与圆O交于不同的两点A、B，当∠AOB=$\frac{π}{2}$时，求k的值．
（2）若k=1，P是直线l上的动点，过P作圆O的两条切线PC、PD，切点为C、D，问：直线CD是否过定点？若过定点，求出定点坐标；若不过定点，说明理由．
（3）若EF、GH为圆O：x2+y2=4的两条相互垂直的弦，垂足为M（1，$\sqrt{2}$），求四边形EGFH的面积的最大值．
13．在△ABC中，已知b=3，c=3$\sqrt{3}$，B=30°，则△ABC的面积S△ABC=$\frac{9}{2}\sqrt{3}$或$\frac{9}{4}\sqrt{3}$．
20．一个多面体的三视图如图所示，则该多面体的体积为（　　）
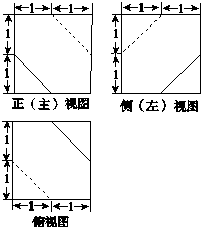
A．$\frac{23}{3}$B．$\frac{22}{3}$C．$\frac{47}{6}$D．7
10．直线x+y=1与直线2x+2y+m2+2=0间距离的最小值为$\sqrt{2}$．
17．若实数x，y满足约束条件$\left\{\begin{array}{l}y≤x\\ y≥-1\\ x+y≤1\end{array}\right.$，则z=2x-y的最大值为（　　）
A．-1B．$\frac{1}{2}$C．5D．7
14．某高中为了解在校高中生对参加某项社会实践活动的意向，拟采用分层抽样的方法从该校三个年级的高中生中抽取一个容量为300的样本进行调查．已知该校高一、高二、高三的人数之比为4：5：6，则应从高一年级抽取80名学生．
11．下列命题中，正确的是（　　）
A．如果直线a∥b，那么a平行于经过b的任何平面
B．如果直线a，b和平面α满足a∥α，b∥α，那么a∥b
C．如果平面α⊥平面β，那么平面α内的所有直线都垂直于平面β
D．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网